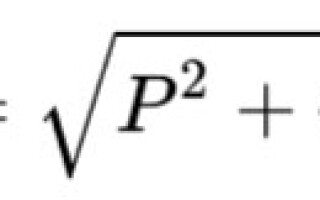ನಾವೆಲ್ಲರೂ ಪ್ರತಿದಿನ ವಿದ್ಯುತ್ ಉಪಕರಣಗಳನ್ನು ನೋಡುತ್ತೇವೆ, ಅವುಗಳಿಲ್ಲದೆ ನಮ್ಮ ಜೀವನವು ನಿಲ್ಲುತ್ತದೆ ಎಂದು ತೋರುತ್ತದೆ. ಮತ್ತು ತಾಂತ್ರಿಕ ಸೂಚನೆಗಳಲ್ಲಿ ಅವುಗಳಲ್ಲಿ ಪ್ರತಿಯೊಂದೂ ಶಕ್ತಿಯನ್ನು ಸೂಚಿಸುತ್ತದೆ. ಇಂದು ನಾವು ಅದು ಏನೆಂದು ಲೆಕ್ಕಾಚಾರ ಮಾಡುತ್ತೇವೆ, ಲೆಕ್ಕಾಚಾರದ ಪ್ರಕಾರಗಳು ಮತ್ತು ವಿಧಾನಗಳನ್ನು ಕಲಿಯುತ್ತೇವೆ.
ವಿಷಯ
ಪರ್ಯಾಯ ವಿದ್ಯುತ್ ಸರ್ಕ್ಯೂಟ್ನಲ್ಲಿ ಪವರ್
ಮುಖ್ಯಕ್ಕೆ ಸಂಪರ್ಕಗೊಂಡಿರುವ ವಿದ್ಯುತ್ ಉಪಕರಣಗಳು ಪರ್ಯಾಯ ವಿದ್ಯುತ್ ಸರ್ಕ್ಯೂಟ್ನಲ್ಲಿ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತವೆ, ಆದ್ದರಿಂದ ನಾವು ಈ ಪರಿಸ್ಥಿತಿಗಳಲ್ಲಿ ಶಕ್ತಿಯನ್ನು ಪರಿಗಣಿಸುತ್ತೇವೆ. ಆದಾಗ್ಯೂ, ಮೊದಲು, ಪರಿಕಲ್ಪನೆಯ ಸಾಮಾನ್ಯ ವ್ಯಾಖ್ಯಾನವನ್ನು ನೀಡೋಣ.
ಶಕ್ತಿ - ವಿದ್ಯುತ್ ಶಕ್ತಿಯ ಪರಿವರ್ತನೆ ಅಥವಾ ಪ್ರಸರಣ ದರವನ್ನು ಪ್ರತಿಬಿಂಬಿಸುವ ಭೌತಿಕ ಪ್ರಮಾಣ.
ಕಿರಿದಾದ ಅರ್ಥದಲ್ಲಿ, ವಿದ್ಯುತ್ ಶಕ್ತಿಯು ಈ ಅವಧಿಗೆ ಒಂದು ನಿರ್ದಿಷ್ಟ ಅವಧಿಯಲ್ಲಿ ನಿರ್ವಹಿಸಿದ ಕೆಲಸದ ಅನುಪಾತವಾಗಿದೆ ಎಂದು ಅವರು ಹೇಳುತ್ತಾರೆ.
ಈ ವ್ಯಾಖ್ಯಾನವನ್ನು ಕಡಿಮೆ ವೈಜ್ಞಾನಿಕವಾಗಿ ಪ್ಯಾರಾಫ್ರೇಸ್ ಮಾಡಲು, ಶಕ್ತಿಯು ನಿರ್ದಿಷ್ಟ ಸಮಯದವರೆಗೆ ಗ್ರಾಹಕರು ಸೇವಿಸುವ ಒಂದು ನಿರ್ದಿಷ್ಟ ಪ್ರಮಾಣದ ಶಕ್ತಿಯಾಗಿದೆ ಎಂದು ಅದು ತಿರುಗುತ್ತದೆ. ಸರಳವಾದ ಉದಾಹರಣೆಯೆಂದರೆ ಸಾಮಾನ್ಯ ಪ್ರಕಾಶಮಾನ ದೀಪ. ಒಂದು ಬೆಳಕಿನ ಬಲ್ಬ್ ತಾನು ಸೇವಿಸುವ ವಿದ್ಯುಚ್ಛಕ್ತಿಯನ್ನು ಶಾಖ ಮತ್ತು ಬೆಳಕಿಗೆ ಪರಿವರ್ತಿಸುವ ದರವು ಅದರ ಶಕ್ತಿಯಾಗಿದೆ. ಅಂತೆಯೇ, ಈ ಸೂಚಕವು ಆರಂಭದಲ್ಲಿ ಬೆಳಕಿನ ಬಲ್ಬ್ಗೆ ಹೆಚ್ಚಾಗಿರುತ್ತದೆ, ಅದು ಹೆಚ್ಚು ಶಕ್ತಿಯನ್ನು ಬಳಸುತ್ತದೆ ಮತ್ತು ಹೆಚ್ಚು ಬೆಳಕನ್ನು ನೀಡುತ್ತದೆ.
ಈ ಸಂದರ್ಭದಲ್ಲಿ ವಿದ್ಯುತ್ ಅನ್ನು ಇನ್ನೊಂದಕ್ಕೆ ಪರಿವರ್ತಿಸುವ ಪ್ರಕ್ರಿಯೆ ಮಾತ್ರವಲ್ಲ (ಬೆಳಕು, ಉಷ್ಣ, ಇತ್ಯಾದಿ.), ಆದರೆ ವಿದ್ಯುತ್ ಮತ್ತು ಕಾಂತೀಯ ಕ್ಷೇತ್ರಗಳ ಆಂದೋಲನದ ಪ್ರಕ್ರಿಯೆ, ಪ್ರಸ್ತುತ ಮತ್ತು ವೋಲ್ಟೇಜ್ ನಡುವೆ ಒಂದು ಹಂತದ ಶಿಫ್ಟ್ ಕಾಣಿಸಿಕೊಳ್ಳುತ್ತದೆ, ಮತ್ತು ಇದನ್ನು ಮತ್ತಷ್ಟು ಲೆಕ್ಕಾಚಾರಗಳಲ್ಲಿ ಗಣನೆಗೆ ತೆಗೆದುಕೊಳ್ಳಬೇಕು.
ಪರ್ಯಾಯ ವಿದ್ಯುತ್ ಸರ್ಕ್ಯೂಟ್ನಲ್ಲಿ ಶಕ್ತಿಯನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡುವಾಗ, ಸಕ್ರಿಯ, ಪ್ರತಿಕ್ರಿಯಾತ್ಮಕ ಮತ್ತು ಪೂರ್ಣ ಘಟಕಗಳನ್ನು ಪ್ರತ್ಯೇಕಿಸಲು ಇದು ರೂಢಿಯಾಗಿದೆ.
ಸಕ್ರಿಯ ಶಕ್ತಿಯ ಪರಿಕಲ್ಪನೆ
ಸಕ್ರಿಯ "ಉಪಯುಕ್ತ" ಶಕ್ತಿಯು ವಿದ್ಯುತ್ ಶಕ್ತಿಯನ್ನು ಇತರ ಶಕ್ತಿಯಾಗಿ ಪರಿವರ್ತಿಸುವ ಪ್ರಕ್ರಿಯೆಯನ್ನು ನೇರವಾಗಿ ನಿರೂಪಿಸುವ ಶಕ್ತಿಯ ಭಾಗವಾಗಿದೆ. ಲ್ಯಾಟಿನ್ ಅಕ್ಷರ P ನಿಂದ ಸೂಚಿಸಲಾಗುತ್ತದೆ ಮತ್ತು ಅಳೆಯಲಾಗುತ್ತದೆ ವ್ಯಾಟ್ಗಳು (ಮಂಗಳವಾರ).
ಸೂತ್ರದ ಪ್ರಕಾರ ಲೆಕ್ಕಹಾಕಲಾಗಿದೆ: P = U⋅I⋅cosφ,
ಅಲ್ಲಿ U ಮತ್ತು I ಕ್ರಮವಾಗಿ ಸರ್ಕ್ಯೂಟ್ನ ವೋಲ್ಟೇಜ್ ಮತ್ತು ಕರೆಂಟ್ನ rms ಮೌಲ್ಯವಾಗಿದೆ, cos φ ಎಂಬುದು ವೋಲ್ಟೇಜ್ ಮತ್ತು ಕರೆಂಟ್ ನಡುವಿನ ಹಂತದ ಕೋನದ ಕೊಸೈನ್ ಆಗಿದೆ.
ಪ್ರಮುಖ! ಹಿಂದೆ ವಿವರಿಸಿದ ಸೂತ್ರವು ಸರ್ಕ್ಯೂಟ್ಗಳನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು ಸೂಕ್ತವಾಗಿದೆ ವೋಲ್ಟೇಜ್ 220V, ಆದಾಗ್ಯೂ, ಶಕ್ತಿಯುತ ಘಟಕಗಳು ಸಾಮಾನ್ಯವಾಗಿ 380V ವೋಲ್ಟೇಜ್ನೊಂದಿಗೆ ನೆಟ್ವರ್ಕ್ ಅನ್ನು ಬಳಸುತ್ತವೆ. ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಅಭಿವ್ಯಕ್ತಿಯನ್ನು ಮೂರು ಅಥವಾ 1.73 ರ ಮೂಲದಿಂದ ಗುಣಿಸಬೇಕು
ಪ್ರತಿಕ್ರಿಯಾತ್ಮಕ ಶಕ್ತಿಯ ಪರಿಕಲ್ಪನೆ
ಪ್ರತಿಕ್ರಿಯಾತ್ಮಕ "ಹಾನಿಕಾರಕ" ಶಕ್ತಿಯು ಇಂಡಕ್ಟಿವ್ ಅಥವಾ ಕೆಪ್ಯಾಸಿಟಿವ್ ಲೋಡ್ನೊಂದಿಗೆ ವಿದ್ಯುತ್ ಉಪಕರಣಗಳ ಕಾರ್ಯಾಚರಣೆಯ ಸಮಯದಲ್ಲಿ ಉತ್ಪತ್ತಿಯಾಗುವ ಶಕ್ತಿಯಾಗಿದೆ ಮತ್ತು ನಡೆಯುತ್ತಿರುವ ವಿದ್ಯುತ್ಕಾಂತೀಯ ಆಂದೋಲನಗಳನ್ನು ಪ್ರತಿಬಿಂಬಿಸುತ್ತದೆ. ಸರಳವಾಗಿ ಹೇಳುವುದಾದರೆ, ಇದು ವಿದ್ಯುತ್ ಮೂಲದಿಂದ ಗ್ರಾಹಕರಿಗೆ ಹಾದುಹೋಗುವ ಶಕ್ತಿಯಾಗಿದೆ, ಮತ್ತು ನಂತರ ನೆಟ್ವರ್ಕ್ಗೆ ಹಿಂತಿರುಗುತ್ತದೆ.
ಸಹಜವಾಗಿ, ವ್ಯವಹಾರದಲ್ಲಿ ಈ ಘಟಕವನ್ನು ಬಳಸುವುದು ಅಸಾಧ್ಯ, ಮೇಲಾಗಿ, ಇದು ಅನೇಕ ವಿಧಗಳಲ್ಲಿ ವಿದ್ಯುತ್ ಸರಬರಾಜು ನೆಟ್ವರ್ಕ್ಗೆ ಹಾನಿ ಮಾಡುತ್ತದೆ, ಆದ್ದರಿಂದ ಅವರು ಸಾಮಾನ್ಯವಾಗಿ ಅದನ್ನು ಸರಿದೂಗಿಸಲು ಪ್ರಯತ್ನಿಸುತ್ತಾರೆ.
ಈ ಮೌಲ್ಯವನ್ನು ಲ್ಯಾಟಿನ್ ಅಕ್ಷರದ Q ನಿಂದ ಸೂಚಿಸಲಾಗುತ್ತದೆ.
ನೆನಪಿಡಿ! ಪ್ರತಿಕ್ರಿಯಾತ್ಮಕ ಶಕ್ತಿಯನ್ನು ಸಾಂಪ್ರದಾಯಿಕ ವ್ಯಾಟ್ಗಳಲ್ಲಿ ಅಳೆಯಲಾಗುವುದಿಲ್ಲ (ಮಂಗಳವಾರ), ಮತ್ತು ಪ್ರತಿಕ್ರಿಯಾತ್ಮಕ ವೋಲ್ಟ್-ಆಂಪಿಯರ್ಗಳಲ್ಲಿ (ವರ್).
ಸೂತ್ರದ ಪ್ರಕಾರ ಲೆಕ್ಕಹಾಕಲಾಗಿದೆ:
Q = U⋅I⋅sinφ,
ಇಲ್ಲಿ U ಮತ್ತು I ಕ್ರಮವಾಗಿ ಸರ್ಕ್ಯೂಟ್ನ ವೋಲ್ಟೇಜ್ ಮತ್ತು ಕರೆಂಟ್ನ rms ಮೌಲ್ಯವಾಗಿದೆ, sinφ ಎಂಬುದು ವೋಲ್ಟೇಜ್ ಮತ್ತು ಕರೆಂಟ್ ನಡುವಿನ ಹಂತದ ಕೋನದ ಸೈನ್ ಆಗಿದೆ.
ಪ್ರಮುಖ! ಲೆಕ್ಕಾಚಾರ ಮಾಡುವಾಗ, ಹಂತದ ಚಲನೆಯನ್ನು ಅವಲಂಬಿಸಿ ಈ ಮೌಲ್ಯವು ಧನಾತ್ಮಕ ಮತ್ತು ಋಣಾತ್ಮಕವಾಗಿರುತ್ತದೆ.
ಕೆಪ್ಯಾಸಿಟಿವ್ ಮತ್ತು ಇಂಡಕ್ಟಿವ್ ಲೋಡ್ಗಳು
ಪ್ರತಿಕ್ರಿಯಾತ್ಮಕ ನಡುವಿನ ಪ್ರಮುಖ ವ್ಯತ್ಯಾಸ (ಕೆಪ್ಯಾಸಿಟಿವ್ ಮತ್ತು ಇಂಡಕ್ಟಿವ್) ಲೋಡ್ಗಳು - ಉಪಸ್ಥಿತಿ, ವಾಸ್ತವವಾಗಿ, ಕೆಪಾಸಿಟನ್ಸ್ ಮತ್ತು ಇಂಡಕ್ಟನ್ಸ್, ಇದು ಶಕ್ತಿಯನ್ನು ಸಂಗ್ರಹಿಸಲು ಮತ್ತು ನಂತರ ಅದನ್ನು ನೆಟ್ವರ್ಕ್ಗೆ ನೀಡುತ್ತದೆ.
ಇಂಡಕ್ಟಿವ್ ಲೋಡ್ ವಿದ್ಯುತ್ ಪ್ರವಾಹದ ಶಕ್ತಿಯನ್ನು ಮೊದಲು ಕಾಂತೀಯ ಕ್ಷೇತ್ರವಾಗಿ ಪರಿವರ್ತಿಸುತ್ತದೆ (ಅರ್ಧ ಚಕ್ರದಲ್ಲಿ), ತದನಂತರ ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ಶಕ್ತಿಯನ್ನು ವಿದ್ಯುತ್ ಪ್ರವಾಹವಾಗಿ ಪರಿವರ್ತಿಸುತ್ತದೆ ಮತ್ತು ಅದನ್ನು ನೆಟ್ವರ್ಕ್ಗೆ ರವಾನಿಸುತ್ತದೆ. ಉದಾಹರಣೆಗಳು ಇಂಡಕ್ಷನ್ ಮೋಟಾರ್ಗಳು, ರಿಕ್ಟಿಫೈಯರ್ಗಳು, ಟ್ರಾನ್ಸ್ಫಾರ್ಮರ್ಗಳು, ವಿದ್ಯುತ್ಕಾಂತಗಳು.
ಪ್ರಮುಖ! ಇಂಡಕ್ಟಿವ್ ಲೋಡ್ ಅನ್ನು ನಿರ್ವಹಿಸುವಾಗ, ಪ್ರಸ್ತುತ ಕರ್ವ್ ಯಾವಾಗಲೂ ವೋಲ್ಟೇಜ್ ಕರ್ವ್ ಅನ್ನು ಅರ್ಧದಷ್ಟು ಚಕ್ರದಿಂದ ಹಿಂದುಳಿಯುತ್ತದೆ.
ಕೆಪ್ಯಾಸಿಟಿವ್ ಲೋಡ್ ವಿದ್ಯುತ್ ಪ್ರವಾಹದ ಶಕ್ತಿಯನ್ನು ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರವಾಗಿ ಪರಿವರ್ತಿಸುತ್ತದೆ ಮತ್ತು ನಂತರ ಪರಿಣಾಮವಾಗಿ ಕ್ಷೇತ್ರದ ಶಕ್ತಿಯನ್ನು ವಿದ್ಯುತ್ ಪ್ರವಾಹವಾಗಿ ಪರಿವರ್ತಿಸುತ್ತದೆ.ಎರಡೂ ಪ್ರಕ್ರಿಯೆಗಳು ಮತ್ತೆ ಅರ್ಧ ಅರ್ಧ ಚಕ್ರಕ್ಕೆ ಮುಂದುವರಿಯುತ್ತವೆ. ಉದಾಹರಣೆಗಳೆಂದರೆ ಕೆಪಾಸಿಟರ್ಗಳು, ಬ್ಯಾಟರಿಗಳು, ಸಿಂಕ್ರೊನಸ್ ಮೋಟಾರ್ಗಳು.
ಪ್ರಮುಖ! ಕೆಪ್ಯಾಸಿಟಿವ್ ಲೋಡ್ ಕಾರ್ಯಾಚರಣೆಯ ಸಮಯದಲ್ಲಿ, ಪ್ರಸ್ತುತ ಕರ್ವ್ ಅರ್ಧದಷ್ಟು ಚಕ್ರದಿಂದ ವೋಲ್ಟೇಜ್ ಕರ್ವ್ ಅನ್ನು ಮುನ್ನಡೆಸುತ್ತದೆ.
ವಿದ್ಯುತ್ ಅಂಶ cosφ
ವಿದ್ಯುತ್ ಅಂಶ cosφ (ಕೊಸೈನ್ ಫೈ ಓದಿ) ವಿದ್ಯುತ್ ಶಕ್ತಿಯ ಬಳಕೆಯ ದಕ್ಷತೆಯನ್ನು ಪ್ರತಿಬಿಂಬಿಸುವ ಸ್ಕೇಲಾರ್ ಭೌತಿಕ ಪ್ರಮಾಣವಾಗಿದೆ. ಸರಳವಾಗಿ ಹೇಳುವುದಾದರೆ, ಗುಣಾಂಕ cosφ ಪ್ರತಿಕ್ರಿಯಾತ್ಮಕ ಭಾಗದ ಉಪಸ್ಥಿತಿ ಮತ್ತು ಒಟ್ಟು ಶಕ್ತಿಗೆ ಸಂಬಂಧಿಸಿದಂತೆ ಸ್ವೀಕರಿಸಿದ ಸಕ್ರಿಯ ಭಾಗದ ಮೌಲ್ಯವನ್ನು ತೋರಿಸುತ್ತದೆ.
ಗುಣಾಂಕ cosφ ಸಕ್ರಿಯ ವಿದ್ಯುತ್ ಶಕ್ತಿ ಮತ್ತು ಸ್ಪಷ್ಟ ವಿದ್ಯುತ್ ಶಕ್ತಿಯ ಅನುಪಾತದ ಮೂಲಕ ಕಂಡುಬರುತ್ತದೆ.
ಸೂಚನೆ! ಹೆಚ್ಚು ನಿಖರವಾದ ಲೆಕ್ಕಾಚಾರದಲ್ಲಿ, ಸೈನುಸಾಯ್ಡ್ನ ರೇಖಾತ್ಮಕವಲ್ಲದ ವಿರೂಪಗಳನ್ನು ಗಣನೆಗೆ ತೆಗೆದುಕೊಳ್ಳಬೇಕು, ಆದಾಗ್ಯೂ, ಅವುಗಳನ್ನು ಸಾಂಪ್ರದಾಯಿಕ ಲೆಕ್ಕಾಚಾರಗಳಲ್ಲಿ ನಿರ್ಲಕ್ಷಿಸಲಾಗುತ್ತದೆ.
ಈ ಗುಣಾಂಕದ ಮೌಲ್ಯವು 0 ರಿಂದ 1 ರವರೆಗೆ ಬದಲಾಗಬಹುದು (ಲೆಕ್ಕಾಚಾರವನ್ನು ಶೇಕಡಾವಾರು ಪ್ರಮಾಣದಲ್ಲಿ ನಡೆಸಿದರೆ, ನಂತರ 0% ರಿಂದ 100% ವರೆಗೆ) ಲೆಕ್ಕಾಚಾರದ ಸೂತ್ರದಿಂದ, ಅದರ ಮೌಲ್ಯವು ಹೆಚ್ಚು, ಸಕ್ರಿಯ ಘಟಕವನ್ನು ಹೆಚ್ಚಿಸುತ್ತದೆ ಎಂದು ಅರ್ಥಮಾಡಿಕೊಳ್ಳುವುದು ಕಷ್ಟವೇನಲ್ಲ, ಅಂದರೆ ಸಾಧನದ ಕಾರ್ಯಕ್ಷಮತೆ ಉತ್ತಮವಾಗಿದೆ.
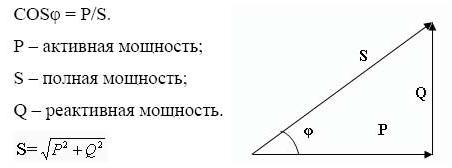
ಒಟ್ಟು ಶಕ್ತಿಯ ಪರಿಕಲ್ಪನೆ. ಶಕ್ತಿ ತ್ರಿಕೋನ
ಸ್ಪಷ್ಟ ಶಕ್ತಿಯು ಕ್ರಮವಾಗಿ ಸಕ್ರಿಯ ಮತ್ತು ಪ್ರತಿಕ್ರಿಯಾತ್ಮಕ ಶಕ್ತಿಯ ವರ್ಗಗಳ ಮೊತ್ತದ ಮೂಲಕ್ಕೆ ಸಮನಾದ ಜ್ಯಾಮಿತೀಯವಾಗಿ ಲೆಕ್ಕಾಚಾರ ಮಾಡಲಾದ ಮೌಲ್ಯವಾಗಿದೆ. ಲ್ಯಾಟಿನ್ ಅಕ್ಷರ S ನೊಂದಿಗೆ ಗೊತ್ತುಪಡಿಸಲಾಗಿದೆ.
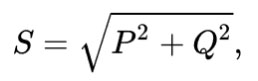
ಕ್ರಮವಾಗಿ ವೋಲ್ಟೇಜ್ ಮತ್ತು ಕರೆಂಟ್ ಅನ್ನು ಗುಣಿಸುವ ಮೂಲಕ ನೀವು ಒಟ್ಟು ಶಕ್ತಿಯನ್ನು ಲೆಕ್ಕ ಹಾಕಬಹುದು.
ಎಸ್ = U⋅I
ಪ್ರಮುಖ! ಸ್ಪಷ್ಟ ಶಕ್ತಿಯನ್ನು ವೋಲ್ಟ್-ಆಂಪಿಯರ್ಗಳಲ್ಲಿ ಅಳೆಯಲಾಗುತ್ತದೆ (VA).
ಪವರ್ ತ್ರಿಕೋನವು ಎಲ್ಲಾ ಹಿಂದೆ ವಿವರಿಸಿದ ಲೆಕ್ಕಾಚಾರಗಳು ಮತ್ತು ಸಕ್ರಿಯ, ಪ್ರತಿಕ್ರಿಯಾತ್ಮಕ ಮತ್ತು ಸ್ಪಷ್ಟ ಶಕ್ತಿಯ ನಡುವಿನ ಸಂಬಂಧಗಳ ಅನುಕೂಲಕರ ಪ್ರಾತಿನಿಧ್ಯವಾಗಿದೆ.
ಕಾಲುಗಳು ಪ್ರತಿಕ್ರಿಯಾತ್ಮಕ ಮತ್ತು ಸಕ್ರಿಯ ಘಟಕಗಳನ್ನು ಪ್ರತಿಬಿಂಬಿಸುತ್ತವೆ, ಹೈಪೊಟೆನ್ಯೂಸ್ - ಒಟ್ಟು ಶಕ್ತಿ. ಜ್ಯಾಮಿತಿಯ ನಿಯಮಗಳ ಪ್ರಕಾರ, φ ಕೋನದ ಕೊಸೈನ್ ಸಕ್ರಿಯ ಮತ್ತು ಒಟ್ಟು ಘಟಕಗಳ ಅನುಪಾತಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ, ಅಂದರೆ, ಇದು ಶಕ್ತಿಯ ಅಂಶವಾಗಿದೆ.
ಸಕ್ರಿಯ, ಪ್ರತಿಕ್ರಿಯಾತ್ಮಕ ಮತ್ತು ಸ್ಪಷ್ಟ ಶಕ್ತಿಯನ್ನು ಕಂಡುಹಿಡಿಯುವುದು ಹೇಗೆ. ಲೆಕ್ಕಾಚಾರದ ಉದಾಹರಣೆ
ಎಲ್ಲಾ ಲೆಕ್ಕಾಚಾರಗಳು ಹಿಂದೆ ಹೇಳಿದ ಸೂತ್ರಗಳು ಮತ್ತು ವಿದ್ಯುತ್ ತ್ರಿಕೋನವನ್ನು ಆಧರಿಸಿವೆ. ಆಚರಣೆಯಲ್ಲಿ ಹೆಚ್ಚಾಗಿ ಎದುರಾಗುವ ಸಮಸ್ಯೆಯನ್ನು ನೋಡೋಣ.
ವಿಶಿಷ್ಟವಾಗಿ, ವಿದ್ಯುತ್ ಉಪಕರಣಗಳನ್ನು ಸಕ್ರಿಯ ಶಕ್ತಿ ಮತ್ತು cosφ ಗುಣಾಂಕದ ಮೌಲ್ಯದೊಂದಿಗೆ ಗುರುತಿಸಲಾಗುತ್ತದೆ. ಈ ಡೇಟಾದೊಂದಿಗೆ, ಪ್ರತಿಕ್ರಿಯಾತ್ಮಕ ಮತ್ತು ಒಟ್ಟು ಘಟಕಗಳನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡುವುದು ಸುಲಭ.
ಇದನ್ನು ಮಾಡಲು, ನಾವು ಗುಣಾಂಕದ cosφ ಮೂಲಕ ಸಕ್ರಿಯ ಶಕ್ತಿಯನ್ನು ವಿಭಜಿಸುತ್ತೇವೆ ಮತ್ತು ಪ್ರಸ್ತುತ ಮತ್ತು ವೋಲ್ಟೇಜ್ನ ಉತ್ಪನ್ನವನ್ನು ಪಡೆಯುತ್ತೇವೆ. ಇದು ಪೂರ್ಣ ಶಕ್ತಿಯಾಗಲಿದೆ.
ಮುಂದೆ, ವಿದ್ಯುತ್ ತ್ರಿಕೋನದ ಆಧಾರದ ಮೇಲೆ, ಸ್ಪಷ್ಟ ಮತ್ತು ಸಕ್ರಿಯ ಶಕ್ತಿಗಳ ಚೌಕಗಳ ನಡುವಿನ ವ್ಯತ್ಯಾಸದ ವರ್ಗಕ್ಕೆ ಸಮಾನವಾದ ಪ್ರತಿಕ್ರಿಯಾತ್ಮಕ ಶಕ್ತಿಯನ್ನು ನಾವು ಕಂಡುಕೊಳ್ಳುತ್ತೇವೆ.
ಆಚರಣೆಯಲ್ಲಿ cosφ ಅನ್ನು ಹೇಗೆ ಅಳೆಯಲಾಗುತ್ತದೆ
cosφ ಗುಣಾಂಕದ ಮೌಲ್ಯವನ್ನು ಸಾಮಾನ್ಯವಾಗಿ ವಿದ್ಯುತ್ ಉಪಕರಣಗಳ ಟ್ಯಾಗ್ಗಳಲ್ಲಿ ಸೂಚಿಸಲಾಗುತ್ತದೆ, ಆದಾಗ್ಯೂ, ಅದನ್ನು ಆಚರಣೆಯಲ್ಲಿ ಅಳೆಯಲು ಅಗತ್ಯವಿದ್ದರೆ, ಅವರು ವಿಶೇಷ ಸಾಧನವನ್ನು ಬಳಸುತ್ತಾರೆ - ಹಂತದ ಮೀಟರ್. ಅಲ್ಲದೆ, ಡಿಜಿಟಲ್ ವ್ಯಾಟ್ಮೀಟರ್ ಈ ಕೆಲಸವನ್ನು ಸುಲಭವಾಗಿ ನಿಭಾಯಿಸುತ್ತದೆ.

ಪಡೆದ ಗುಣಾಂಕ cosφ ಸಾಕಷ್ಟು ಕಡಿಮೆಯಿದ್ದರೆ, ಅದನ್ನು ಪ್ರಾಯೋಗಿಕವಾಗಿ ಸರಿದೂಗಿಸಬಹುದು. ಸರ್ಕ್ಯೂಟ್ನಲ್ಲಿ ಹೆಚ್ಚುವರಿ ಸಾಧನಗಳನ್ನು ಸೇರಿಸುವ ಮೂಲಕ ಇದನ್ನು ಮುಖ್ಯವಾಗಿ ಮಾಡಲಾಗುತ್ತದೆ.
- ಪ್ರತಿಕ್ರಿಯಾತ್ಮಕ ಘಟಕವನ್ನು ಸರಿಪಡಿಸಲು ಅಗತ್ಯವಿದ್ದರೆ, ಈಗಾಗಲೇ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತಿರುವ ಸಾಧನಕ್ಕೆ ವಿರುದ್ಧವಾಗಿ ಕಾರ್ಯನಿರ್ವಹಿಸುವ ಸರ್ಕ್ಯೂಟ್ನಲ್ಲಿ ಪ್ರತಿಕ್ರಿಯಾತ್ಮಕ ಅಂಶವನ್ನು ಸೇರಿಸಬೇಕು. ಇಂಡಕ್ಷನ್ ಮೋಟರ್ನ ಕಾರ್ಯಾಚರಣೆಯನ್ನು ಸರಿದೂಗಿಸಲು, ಉದಾಹರಣೆಗೆ ಇಂಡಕ್ಟಿವ್ ಲೋಡ್, ಕೆಪಾಸಿಟರ್ ಅನ್ನು ಸಮಾನಾಂತರವಾಗಿ ಸಂಪರ್ಕಿಸಲಾಗಿದೆ. ಸಿಂಕ್ರೊನಸ್ ಮೋಟರ್ ಅನ್ನು ಸರಿದೂಗಿಸಲು ವಿದ್ಯುತ್ಕಾಂತವನ್ನು ಸಂಪರ್ಕಿಸಲಾಗಿದೆ.
- ರೇಖಾತ್ಮಕವಲ್ಲದ ಸಮಸ್ಯೆಗಳನ್ನು ಸರಿಪಡಿಸಲು ಅಗತ್ಯವಿದ್ದರೆ, ನಿಷ್ಕ್ರಿಯ cosφ ಸರಿಪಡಿಸುವಿಕೆಯನ್ನು ಸರ್ಕ್ಯೂಟ್ಗೆ ಪರಿಚಯಿಸಲಾಗುತ್ತದೆ, ಉದಾಹರಣೆಗೆ, ಇದು ಲೋಡ್ನೊಂದಿಗೆ ಸರಣಿಯಲ್ಲಿ ಸಂಪರ್ಕಗೊಂಡಿರುವ ಹೆಚ್ಚಿನ ಇಂಡಕ್ಟನ್ಸ್ ಚಾಕ್ ಆಗಿರಬಹುದು.
ವಿದ್ಯುತ್ ಉಪಕರಣಗಳ ಪ್ರಮುಖ ಸೂಚಕಗಳಲ್ಲಿ ಪವರ್ ಒಂದಾಗಿದೆ, ಆದ್ದರಿಂದ ಅದು ಏನು ಮತ್ತು ಅದನ್ನು ಹೇಗೆ ಲೆಕ್ಕ ಹಾಕಲಾಗುತ್ತದೆ ಎಂಬುದನ್ನು ತಿಳಿದುಕೊಳ್ಳುವುದು ಶಾಲಾ ಮಕ್ಕಳಿಗೆ ಮತ್ತು ತಂತ್ರಜ್ಞಾನದಲ್ಲಿ ಪರಿಣತಿ ಹೊಂದಿರುವ ಜನರಿಗೆ ಮಾತ್ರವಲ್ಲದೆ ನಮ್ಮಲ್ಲಿ ಪ್ರತಿಯೊಬ್ಬರಿಗೂ ಸಹ ಉಪಯುಕ್ತವಾಗಿದೆ.
ಇದೇ ರೀತಿಯ ಲೇಖನಗಳು: