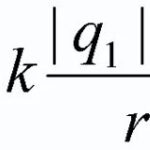ಎಲೆಕ್ಟ್ರೋಸ್ಟಾಟಿಕ್ಸ್ ಮತ್ತು ಎಲೆಕ್ಟ್ರೋಡೈನಾಮಿಕ್ಸ್ ಸಿದ್ಧಾಂತದ ಪ್ರಮುಖ ಅಡಿಪಾಯಗಳಲ್ಲಿ ವಿದ್ಯುತ್ ವಿಭವದ ಪರಿಕಲ್ಪನೆಯು ಒಂದು. ಭೌತಶಾಸ್ತ್ರದ ಈ ಶಾಖೆಗಳ ಹೆಚ್ಚಿನ ಅಧ್ಯಯನಕ್ಕೆ ಅದರ ಸಾರವನ್ನು ಅರ್ಥಮಾಡಿಕೊಳ್ಳುವುದು ಅವಶ್ಯಕ ಸ್ಥಿತಿಯಾಗಿದೆ.
ವಿದ್ಯುತ್ ಸಾಮರ್ಥ್ಯ ಎಂದರೇನು
ಯುನಿಟ್ ಚಾರ್ಜ್ q ಅನ್ನು ಸ್ಥಿರ ಚಾರ್ಜ್ Q ನಿಂದ ರಚಿಸಲಾದ ಕ್ಷೇತ್ರದಲ್ಲಿ ಇರಿಸೋಣ, ಅದು ಪರಿಣಾಮ ಬೀರುತ್ತದೆ ಕೂಲಂಬ್ ಫೋರ್ಸ್ F=k*Qq/r.
ಇಲ್ಲಿ ಮತ್ತು ಕೆಳಗೆ k=((1/4)*π* ε* ε), ಅಲ್ಲಿ ε0 — ವಿದ್ಯುತ್ ಸ್ಥಿರ (8.85*10-12 F/m), ε ಆಗಿರುವಾಗ ಮಧ್ಯಮ ಡೈಎಲೆಕ್ಟ್ರಿಕ್ ಸ್ಥಿರ.
ಕೊಡುಗೆ ನೀಡಿದ್ದಾರೆ ಶುಲ್ಕ ಈ ಶಕ್ತಿಯ ಕ್ರಿಯೆಯ ಅಡಿಯಲ್ಲಿ, ಅದು ಚಲಿಸಬಹುದು, ಮತ್ತು ಬಲವು ಒಂದು ನಿರ್ದಿಷ್ಟ ಪ್ರಮಾಣದ ಕೆಲಸವನ್ನು ಮಾಡುತ್ತದೆ. ಇದರರ್ಥ ಎರಡು ಚಾರ್ಜ್ಗಳ ವ್ಯವಸ್ಥೆಯು ಸಂಭಾವ್ಯ ಶಕ್ತಿಯನ್ನು ಹೊಂದಿದ್ದು ಅದು ಎರಡೂ ಚಾರ್ಜ್ಗಳ ಪ್ರಮಾಣ ಮತ್ತು ಅವುಗಳ ನಡುವಿನ ಅಂತರವನ್ನು ಅವಲಂಬಿಸಿರುತ್ತದೆ ಮತ್ತು ಈ ಸಂಭಾವ್ಯ ಶಕ್ತಿಯ ಪ್ರಮಾಣವು ಚಾರ್ಜ್ q ನ ಪ್ರಮಾಣವನ್ನು ಅವಲಂಬಿಸಿರುವುದಿಲ್ಲ. ಇಲ್ಲಿ ವಿದ್ಯುತ್ ವಿಭವದ ವ್ಯಾಖ್ಯಾನವನ್ನು ಪರಿಚಯಿಸಲಾಗಿದೆ - ಇದು ಕ್ಷೇತ್ರದ ಸಂಭಾವ್ಯ ಶಕ್ತಿಯ ಅನುಪಾತಕ್ಕೆ ಚಾರ್ಜ್ನ ಪ್ರಮಾಣಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ:
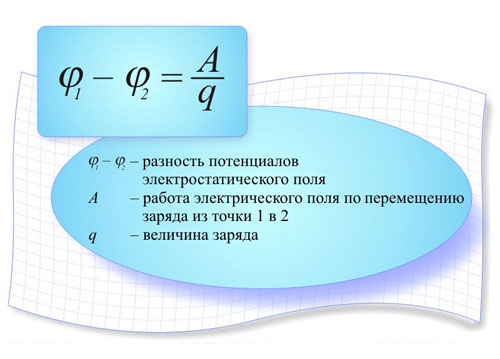
φ=W/q,
ಇಲ್ಲಿ W ಎಂಬುದು ಚಾರ್ಜ್ಗಳ ವ್ಯವಸ್ಥೆಯಿಂದ ರಚಿಸಲ್ಪಟ್ಟ ಕ್ಷೇತ್ರದ ಸಂಭಾವ್ಯ ಶಕ್ತಿಯಾಗಿದೆ ಮತ್ತು ಸಂಭಾವ್ಯತೆಯು ಕ್ಷೇತ್ರದ ಶಕ್ತಿಯ ಲಕ್ಷಣವಾಗಿದೆ. ಸ್ವಲ್ಪ ದೂರದವರೆಗೆ ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರದಲ್ಲಿ ಚಾರ್ಜ್ q ಅನ್ನು ಸರಿಸಲು, ಕೂಲಂಬ್ ಪಡೆಗಳನ್ನು ಜಯಿಸಲು ನಿರ್ದಿಷ್ಟ ಪ್ರಮಾಣದ ಕೆಲಸವನ್ನು ವ್ಯಯಿಸುವುದು ಅವಶ್ಯಕ. ಒಂದು ಬಿಂದುವಿನ ವಿಭವವು ಈ ಬಿಂದುವಿನಿಂದ ಅನಂತಕ್ಕೆ ಯೂನಿಟ್ ಚಾರ್ಜ್ ಅನ್ನು ಸರಿಸಲು ಖರ್ಚು ಮಾಡಬೇಕಾದ ಕೆಲಸಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ. ಹಾಗೆ ಮಾಡುವಾಗ, ಇದನ್ನು ಗಮನಿಸಬೇಕು:
- ಈ ಕೆಲಸವು ಚಾರ್ಜ್ನ ಸಂಭಾವ್ಯ ಶಕ್ತಿಯ ಇಳಿಕೆಗೆ ಸಮನಾಗಿರುತ್ತದೆ (A=W2-ಡಬ್ಲ್ಯೂ1);
- ಕೆಲಸವು ಚಾರ್ಜ್ನ ಪಥವನ್ನು ಅವಲಂಬಿಸಿರುವುದಿಲ್ಲ.
SI ವ್ಯವಸ್ಥೆಯಲ್ಲಿ, ಸಂಭಾವ್ಯತೆಯ ಘಟಕವು ಒಂದು ವೋಲ್ಟ್ ಆಗಿದೆ (ರಷ್ಯಾದ ಸಾಹಿತ್ಯದಲ್ಲಿ ಇದನ್ನು V ಅಕ್ಷರದಿಂದ ಸೂಚಿಸಲಾಗುತ್ತದೆ, ವಿದೇಶಿ ಸಾಹಿತ್ಯದಲ್ಲಿ - V). 1 V \u003d 1J / 1 C, ಅಂದರೆ, 1 C ಚಾರ್ಜ್ ಅನ್ನು ಅನಂತಕ್ಕೆ ಸರಿಸಲು 1 ಜೌಲ್ ತೆಗೆದುಕೊಂಡರೆ ನಾವು 1 ವೋಲ್ಟ್ ಬಿಂದುವಿನ ಸಂಭಾವ್ಯತೆಯ ಬಗ್ಗೆ ಮಾತನಾಡಬಹುದು. ಎಲೆಕ್ಟ್ರಿಕಲ್ ಎಂಜಿನಿಯರಿಂಗ್ ಅಭಿವೃದ್ಧಿಗೆ ಮಹತ್ವದ ಕೊಡುಗೆ ನೀಡಿದ ಇಟಾಲಿಯನ್ ಭೌತಶಾಸ್ತ್ರಜ್ಞ ಅಲೆಸ್ಸಾಂಡ್ರೊ ವೋಲ್ಟಾ ಅವರ ಗೌರವಾರ್ಥವಾಗಿ ಈ ಹೆಸರನ್ನು ಆಯ್ಕೆ ಮಾಡಲಾಗಿದೆ.
ಸಂಭಾವ್ಯತೆ ಏನೆಂಬುದನ್ನು ದೃಶ್ಯೀಕರಿಸಲು, ಅದನ್ನು ಎರಡು ದೇಹಗಳ ತಾಪಮಾನ ಅಥವಾ ಬಾಹ್ಯಾಕಾಶದಲ್ಲಿ ವಿವಿಧ ಹಂತಗಳಲ್ಲಿ ಅಳೆಯುವ ತಾಪಮಾನದೊಂದಿಗೆ ಹೋಲಿಸಬಹುದು. ತಾಪಮಾನವು ವಸ್ತುಗಳ ತಾಪನದ ಅಳತೆಯಾಗಿದೆ, ಮತ್ತು ಸಂಭಾವ್ಯತೆಯು ವಿದ್ಯುತ್ ಚಾರ್ಜ್ನ ಅಳತೆಯಾಗಿದೆ. ಒಂದು ದೇಹವು ಇನ್ನೊಂದಕ್ಕಿಂತ ಹೆಚ್ಚು ಬಿಸಿಯಾಗುತ್ತದೆ ಎಂದು ಹೇಳಲಾಗುತ್ತದೆ, ಒಂದು ದೇಹವು ಹೆಚ್ಚು ಮತ್ತು ಇನ್ನೊಂದು ಕಡಿಮೆ ಚಾರ್ಜ್ ಆಗುತ್ತದೆ ಎಂದು ಕೂಡ ಹೇಳಬಹುದು. ಈ ದೇಹಗಳು ವಿಭಿನ್ನ ಸಾಮರ್ಥ್ಯವನ್ನು ಹೊಂದಿವೆ.
ವಿಭವದ ಮೌಲ್ಯವು ನಿರ್ದೇಶಾಂಕ ವ್ಯವಸ್ಥೆಯ ಆಯ್ಕೆಯ ಮೇಲೆ ಅವಲಂಬಿತವಾಗಿರುತ್ತದೆ, ಆದ್ದರಿಂದ ಕೆಲವು ಮಟ್ಟದ ಅಗತ್ಯವಿದೆ, ಅದನ್ನು ಶೂನ್ಯವಾಗಿ ತೆಗೆದುಕೊಳ್ಳಬೇಕು. ತಾಪಮಾನವನ್ನು ಅಳೆಯುವಾಗ, ಉದಾಹರಣೆಗೆ, ಕರಗುವ ಮಂಜುಗಡ್ಡೆಯ ತಾಪಮಾನವನ್ನು ಬೇಸ್ಲೈನ್ ಆಗಿ ತೆಗೆದುಕೊಳ್ಳಬಹುದು.ಸಂಭಾವ್ಯತೆಗಾಗಿ, ಅನಂತ ದೂರದ ಬಿಂದುವಿನ ಸಂಭಾವ್ಯತೆಯನ್ನು ಸಾಮಾನ್ಯವಾಗಿ ಶೂನ್ಯ ಮಟ್ಟವಾಗಿ ತೆಗೆದುಕೊಳ್ಳಲಾಗುತ್ತದೆ, ಆದರೆ ಕೆಲವು ಸಮಸ್ಯೆಗಳನ್ನು ಪರಿಹರಿಸಲು, ಉದಾಹರಣೆಗೆ, ನೆಲದ ಸಾಮರ್ಥ್ಯ ಅಥವಾ ಕೆಪಾಸಿಟರ್ ಪ್ಲೇಟ್ಗಳ ಸಂಭಾವ್ಯತೆಯನ್ನು ಶೂನ್ಯವೆಂದು ಪರಿಗಣಿಸಬಹುದು.
ಸಂಭಾವ್ಯ ಗುಣಲಕ್ಷಣಗಳು
ಸಂಭಾವ್ಯತೆಯ ಪ್ರಮುಖ ಗುಣಲಕ್ಷಣಗಳಲ್ಲಿ, ಈ ಕೆಳಗಿನವುಗಳನ್ನು ಗಮನಿಸಬೇಕು:
- ಕ್ಷೇತ್ರವನ್ನು ಹಲವಾರು ಚಾರ್ಜ್ಗಳಿಂದ ರಚಿಸಿದರೆ, ಒಂದು ನಿರ್ದಿಷ್ಟ ಹಂತದಲ್ಲಿ ಸಂಭಾವ್ಯತೆಯು ಬೀಜಗಣಿತಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ (ಚಾರ್ಜ್ನ ಚಿಹ್ನೆಯನ್ನು ಗಣನೆಗೆ ತೆಗೆದುಕೊಂಡು) ಪ್ರತಿಯೊಂದು ಚಾರ್ಜ್ಗಳು φ=φ ರಚಿಸಲಾದ ವಿಭವಗಳ ಮೊತ್ತ1+φ2+φ3+φ4+φ5+…+φಎನ್;
- ಚಾರ್ಜ್ಗಳಿಂದ ದೂರವು ಚಾರ್ಜ್ಗಳನ್ನು ಪಾಯಿಂಟ್ ಚಾರ್ಜ್ಗಳೆಂದು ಪರಿಗಣಿಸಬಹುದಾದರೆ, ಒಟ್ಟು ಸಂಭಾವ್ಯತೆಯನ್ನು φ=k*(q) ಸೂತ್ರದಿಂದ ಲೆಕ್ಕಹಾಕಲಾಗುತ್ತದೆ1/ಆರ್1+q2/ಆರ್2+q3/ಆರ್3+…+qಎನ್/ಆರ್ಎನ್), ಇಲ್ಲಿ r ಎಂಬುದು ಅನುಗುಣವಾದ ಚಾರ್ಜ್ನಿಂದ ದೂರವಾಗಿದ್ದು ನಂತರ ಪರಿಗಣಿಸಲಾದ ಬಿಂದುವಾಗಿದೆ.
ಕ್ಷೇತ್ರವು ವಿದ್ಯುತ್ ದ್ವಿಧ್ರುವಿಯಿಂದ ರೂಪುಗೊಂಡಿದ್ದರೆ (ವಿರುದ್ಧ ಚಿಹ್ನೆಯ ಎರಡು ಸಂಪರ್ಕಿತ ಚಾರ್ಜ್ಗಳು), ನಂತರ ದ್ವಿಧ್ರುವಿಯಿಂದ r ದೂರದಲ್ಲಿರುವ ಯಾವುದೇ ಹಂತದಲ್ಲಿ ಸಂಭಾವ್ಯತೆಯು φ=k*p*cosά/r ಗೆ ಸಮನಾಗಿರುತ್ತದೆ.2, ಎಲ್ಲಿ:
- p ಎಂಬುದು ದ್ವಿಧ್ರುವಿಯ ವಿದ್ಯುತ್ ತೋಳು, q*l ಗೆ ಸಮನಾಗಿರುತ್ತದೆ, ಇಲ್ಲಿ l ಎಂಬುದು ಶುಲ್ಕಗಳ ನಡುವಿನ ಅಂತರವಾಗಿದೆ;
- r ಎಂಬುದು ದ್ವಿಧ್ರುವಿಯ ಅಂತರ;
- ά ಎಂಬುದು ದ್ವಿಧ್ರುವಿ ತೋಳು ಮತ್ತು ತ್ರಿಜ್ಯದ ವೆಕ್ಟರ್ ಆರ್ ನಡುವಿನ ಕೋನವಾಗಿದೆ.
ಬಿಂದುವು ದ್ವಿಧ್ರುವಿಯ ಅಕ್ಷದ ಮೇಲೆ ಇದ್ದರೆ, cosά=1 ಮತ್ತು φ=k*p/r2.
ಸಂಭಾವ್ಯ ವ್ಯತ್ಯಾಸ
ಎರಡು ಬಿಂದುಗಳು ಒಂದು ನಿರ್ದಿಷ್ಟ ಸಾಮರ್ಥ್ಯವನ್ನು ಹೊಂದಿದ್ದರೆ ಮತ್ತು ಅವು ಸಮಾನವಾಗಿಲ್ಲದಿದ್ದರೆ, ಎರಡು ಬಿಂದುಗಳ ನಡುವೆ ಸಂಭಾವ್ಯ ವ್ಯತ್ಯಾಸವಿದೆ ಎಂದು ಅವರು ಹೇಳುತ್ತಾರೆ. ಬಿಂದುಗಳ ನಡುವೆ ಸಂಭಾವ್ಯ ವ್ಯತ್ಯಾಸವು ಸಂಭವಿಸುತ್ತದೆ:
- ಅವರ ಸಾಮರ್ಥ್ಯವನ್ನು ವಿವಿಧ ಚಿಹ್ನೆಗಳ ಆರೋಪಗಳಿಂದ ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ;
- ಯಾವುದೇ ಚಿಹ್ನೆಯ ಚಾರ್ಜ್ನಿಂದ ಸಂಭಾವ್ಯತೆಯನ್ನು ಹೊಂದಿರುವ ಬಿಂದು ಮತ್ತು ಶೂನ್ಯ ವಿಭವದೊಂದಿಗೆ ಬಿಂದು;
- ಒಂದೇ ಚಿಹ್ನೆಯ ಸಾಮರ್ಥ್ಯವನ್ನು ಹೊಂದಿರುವ ಬಿಂದುಗಳು, ಆದರೆ ಸಂಪೂರ್ಣ ಮೌಲ್ಯದಲ್ಲಿ ಭಿನ್ನವಾಗಿರುತ್ತವೆ.
ಅಂದರೆ, ಸಂಭಾವ್ಯ ವ್ಯತ್ಯಾಸವು ನಿರ್ದೇಶಾಂಕ ವ್ಯವಸ್ಥೆಯ ಆಯ್ಕೆಯ ಮೇಲೆ ಅವಲಂಬಿತವಾಗಿರುವುದಿಲ್ಲ.ಶೂನ್ಯ ಮಾರ್ಕ್ಗೆ (ಉದಾಹರಣೆಗೆ, ಸಮುದ್ರ ಮಟ್ಟ) ಹೋಲಿಸಿದರೆ ವಿಭಿನ್ನ ಎತ್ತರದಲ್ಲಿರುವ ನೀರಿನ ಪೂಲ್ಗಳೊಂದಿಗೆ ಸಾದೃಶ್ಯವನ್ನು ಎಳೆಯಬಹುದು.
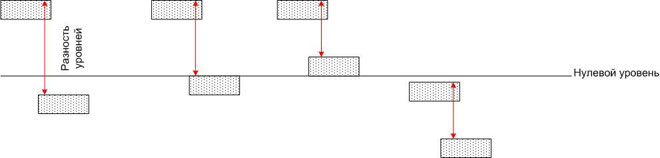
ಪ್ರತಿ ಪೂಲ್ನ ನೀರು ಒಂದು ನಿರ್ದಿಷ್ಟ ಸಂಭಾವ್ಯ ಶಕ್ತಿಯನ್ನು ಹೊಂದಿರುತ್ತದೆ, ಆದರೆ ನೀವು ಯಾವುದೇ ಎರಡು ಪೂಲ್ಗಳನ್ನು ಟ್ಯೂಬ್ನೊಂದಿಗೆ ಸಂಪರ್ಕಿಸಿದರೆ, ಪ್ರತಿಯೊಂದರಲ್ಲೂ ನೀರಿನ ಹರಿವು ಇರುತ್ತದೆ, ಅದರ ಹರಿವಿನ ಪ್ರಮಾಣವು ಟ್ಯೂಬ್ನ ಗಾತ್ರದಿಂದ ಮಾತ್ರವಲ್ಲದೆ ನಿರ್ಧರಿಸಲ್ಪಡುತ್ತದೆ. , ಆದರೆ ಭೂಮಿಯ ಗುರುತ್ವಾಕರ್ಷಣೆಯ ಕ್ಷೇತ್ರದಲ್ಲಿ ಸಂಭಾವ್ಯ ಶಕ್ತಿಗಳ ವ್ಯತ್ಯಾಸದಿಂದ (ಅಂದರೆ, ಎತ್ತರ ವ್ಯತ್ಯಾಸ). ಈ ಸಂದರ್ಭದಲ್ಲಿ ಸಂಭಾವ್ಯ ಶಕ್ತಿಗಳ ಸಂಪೂರ್ಣ ಮೌಲ್ಯವು ಅಪ್ರಸ್ತುತವಾಗುತ್ತದೆ.
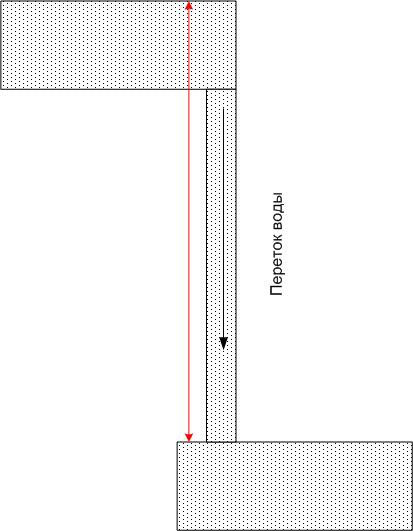
ಅದೇ ರೀತಿಯಲ್ಲಿ, ನೀವು ಕಂಡಕ್ಟರ್ನೊಂದಿಗೆ ವಿಭಿನ್ನ ಸಾಮರ್ಥ್ಯದೊಂದಿಗೆ ಎರಡು ಬಿಂದುಗಳನ್ನು ಸಂಪರ್ಕಿಸಿದರೆ, ಅದು ಹರಿಯುತ್ತದೆ ವಿದ್ಯುತ್, ಕಂಡಕ್ಟರ್ನ ಪ್ರತಿರೋಧದಿಂದ ಮಾತ್ರ ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ, ಆದರೆ ಸಂಭಾವ್ಯ ವ್ಯತ್ಯಾಸದಿಂದ (ಆದರೆ ಅವರ ಸಂಪೂರ್ಣ ಮೌಲ್ಯದಿಂದ ಅಲ್ಲ). ನೀರಿನೊಂದಿಗೆ ಸಾದೃಶ್ಯವನ್ನು ಮುಂದುವರಿಸುತ್ತಾ, ಮೇಲಿನ ಕೊಳದಲ್ಲಿನ ನೀರು ಶೀಘ್ರದಲ್ಲೇ ಖಾಲಿಯಾಗುತ್ತದೆ ಎಂದು ನಾವು ಹೇಳಬಹುದು ಮತ್ತು ನೀರನ್ನು ಹಿಂದಕ್ಕೆ ಚಲಿಸುವ ಯಾವುದೇ ಶಕ್ತಿ ಇಲ್ಲದಿದ್ದರೆ (ಉದಾಹರಣೆಗೆ, ಪಂಪ್), ನಂತರ ಹರಿವು ಬಹಳ ಬೇಗನೆ ನಿಲ್ಲುತ್ತದೆ.
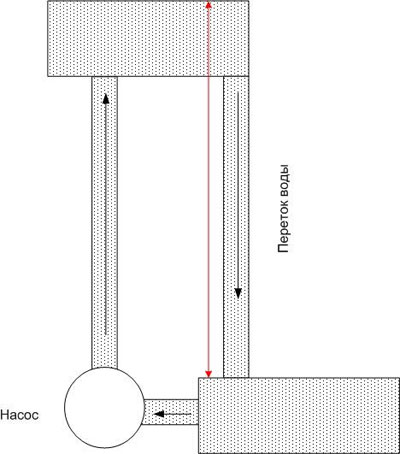
ಆದ್ದರಿಂದ ಇದು ಎಲೆಕ್ಟ್ರಿಕ್ ಸರ್ಕ್ಯೂಟ್ನಲ್ಲಿದೆ - ಒಂದು ನಿರ್ದಿಷ್ಟ ಮಟ್ಟದಲ್ಲಿ ಸಂಭಾವ್ಯ ವ್ಯತ್ಯಾಸವನ್ನು ಕಾಪಾಡಿಕೊಳ್ಳಲು, ಚಾರ್ಜ್ಗಳನ್ನು (ಹೆಚ್ಚು ನಿಖರವಾಗಿ, ಚಾರ್ಜ್ ಕ್ಯಾರಿಯರ್ಗಳು) ಅತ್ಯಧಿಕ ಸಾಮರ್ಥ್ಯವಿರುವ ಬಿಂದುವಿಗೆ ವರ್ಗಾಯಿಸುವ ಶಕ್ತಿಯ ಅಗತ್ಯವಿದೆ. ಈ ಬಲವನ್ನು ಎಲೆಕ್ಟ್ರೋಮೋಟಿವ್ ಫೋರ್ಸ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ಮತ್ತು ಇದನ್ನು ಇಎಮ್ಎಫ್ ಎಂದು ಸಂಕ್ಷೇಪಿಸಲಾಗುತ್ತದೆ. ಇಎಮ್ಎಫ್ ವಿಭಿನ್ನ ಸ್ವಭಾವವನ್ನು ಹೊಂದಿರಬಹುದು - ಎಲೆಕ್ಟ್ರೋಕೆಮಿಕಲ್, ಎಲೆಕ್ಟ್ರೋಮ್ಯಾಗ್ನೆಟಿಕ್, ಇತ್ಯಾದಿ.
ಪ್ರಾಯೋಗಿಕವಾಗಿ, ಇದು ಮುಖ್ಯವಾಗಿ ಚಾರ್ಜ್ ಕ್ಯಾರಿಯರ್ಗಳ ಪಥದ ಆರಂಭಿಕ ಮತ್ತು ಅಂತಿಮ ಬಿಂದುಗಳ ನಡುವಿನ ಸಂಭಾವ್ಯ ವ್ಯತ್ಯಾಸವಾಗಿದೆ. ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಈ ವ್ಯತ್ಯಾಸವನ್ನು ವೋಲ್ಟೇಜ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ, ಮತ್ತು SI ನಲ್ಲಿ ಇದನ್ನು ವೋಲ್ಟ್ಗಳಲ್ಲಿ ಅಳೆಯಲಾಗುತ್ತದೆ.1 ಕೂಲಂಬ್ ಚಾರ್ಜ್ ಅನ್ನು ಒಂದು ಬಿಂದುವಿನಿಂದ ಇನ್ನೊಂದಕ್ಕೆ ಚಲಿಸುವಾಗ ಕ್ಷೇತ್ರವು 1 ಜೌಲ್ ಕೆಲಸ ಮಾಡಿದರೆ ನಾವು 1 ವೋಲ್ಟ್ ವೋಲ್ಟೇಜ್ ಬಗ್ಗೆ ಮಾತನಾಡಬಹುದು, ಅಂದರೆ, 1V \u003d 1J / 1C, ಮತ್ತು J / C ಯು ಯುನಿಟ್ ಆಗಿರಬಹುದು. ಸಂಭಾವ್ಯ ವ್ಯತ್ಯಾಸ.
ಈಕ್ವಿಪೊಟೆನ್ಷಿಯಲ್ ಮೇಲ್ಮೈಗಳು
ಹಲವಾರು ಬಿಂದುಗಳ ಸಾಮರ್ಥ್ಯವು ಒಂದೇ ಆಗಿದ್ದರೆ ಮತ್ತು ಈ ಬಿಂದುಗಳು ಮೇಲ್ಮೈಯನ್ನು ರೂಪಿಸಿದರೆ, ಅಂತಹ ಮೇಲ್ಮೈಯನ್ನು ಈಕ್ವಿಪೊಟೆನ್ಷಿಯಲ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಅಂತಹ ಆಸ್ತಿಯು, ಉದಾಹರಣೆಗೆ, ವಿದ್ಯುದಾವೇಶದ ಸುತ್ತ ಸುತ್ತುವರಿದ ಗೋಳವನ್ನು ಹೊಂದಿದೆ, ಏಕೆಂದರೆ ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರವು ಎಲ್ಲಾ ದಿಕ್ಕುಗಳಲ್ಲಿಯೂ ಸಮಾನವಾಗಿ ದೂರದೊಂದಿಗೆ ಕಡಿಮೆಯಾಗುತ್ತದೆ.
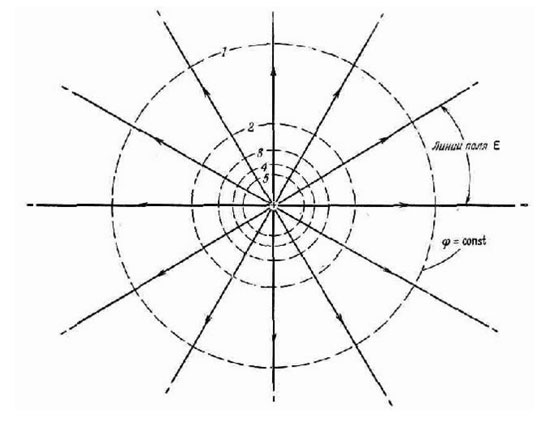
ಈ ಮೇಲ್ಮೈಯ ಎಲ್ಲಾ ಬಿಂದುಗಳು ಒಂದೇ ಸಂಭಾವ್ಯ ಶಕ್ತಿಯನ್ನು ಹೊಂದಿವೆ, ಆದ್ದರಿಂದ ಅಂತಹ ಗೋಳದ ಮೇಲೆ ಚಾರ್ಜ್ ಅನ್ನು ಚಲಿಸುವಾಗ, ಯಾವುದೇ ಕೆಲಸವನ್ನು ಖರ್ಚು ಮಾಡಲಾಗುವುದಿಲ್ಲ. ಹಲವಾರು ಶುಲ್ಕಗಳ ವ್ಯವಸ್ಥೆಗಳ ಈಕ್ವಿಪೊಟೆನ್ಷಿಯಲ್ ಮೇಲ್ಮೈಗಳು ಹೆಚ್ಚು ಸಂಕೀರ್ಣವಾದ ಆಕಾರವನ್ನು ಹೊಂದಿವೆ, ಆದರೆ ಅವುಗಳು ಒಂದು ಆಸಕ್ತಿದಾಯಕ ಆಸ್ತಿಯನ್ನು ಹೊಂದಿವೆ - ಅವು ಎಂದಿಗೂ ಛೇದಿಸುವುದಿಲ್ಲ. ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರದ ಬಲದ ರೇಖೆಗಳು ಯಾವಾಗಲೂ ಅವುಗಳ ಪ್ರತಿಯೊಂದು ಬಿಂದುಗಳಲ್ಲಿ ಒಂದೇ ಸಂಭಾವ್ಯತೆಯನ್ನು ಹೊಂದಿರುವ ಮೇಲ್ಮೈಗಳಿಗೆ ಲಂಬವಾಗಿರುತ್ತವೆ. ಈಕ್ವಿಪೊಟೆನ್ಷಿಯಲ್ ಮೇಲ್ಮೈಯನ್ನು ಸಮತಲದಿಂದ ಕತ್ತರಿಸಿದರೆ, ಸಮಾನ ವಿಭವಗಳ ರೇಖೆಯನ್ನು ಪಡೆಯಲಾಗುತ್ತದೆ. ಇದು ಈಕ್ವಿಪೊಟೆನ್ಷಿಯಲ್ ಮೇಲ್ಮೈಯಂತೆಯೇ ಅದೇ ಗುಣಲಕ್ಷಣಗಳನ್ನು ಹೊಂದಿದೆ. ಆಚರಣೆಯಲ್ಲಿ, ಉದಾಹರಣೆಗೆ, ಸ್ಥಾಯೀವಿದ್ಯುತ್ತಿನ ಕ್ಷೇತ್ರದಲ್ಲಿ ಇರಿಸಲಾದ ವಾಹಕದ ಮೇಲ್ಮೈಯಲ್ಲಿರುವ ಬಿಂದುಗಳು ಸಮಾನ ಸಾಮರ್ಥ್ಯವನ್ನು ಹೊಂದಿವೆ.
ಸಂಭಾವ್ಯ ಮತ್ತು ಸಂಭಾವ್ಯ ವ್ಯತ್ಯಾಸದ ಪರಿಕಲ್ಪನೆಯೊಂದಿಗೆ ವ್ಯವಹರಿಸಿದ ನಂತರ, ನೀವು ವಿದ್ಯುತ್ ವಿದ್ಯಮಾನಗಳ ಹೆಚ್ಚಿನ ಅಧ್ಯಯನಕ್ಕೆ ಮುಂದುವರಿಯಬಹುದು. ಆದರೆ ಮೊದಲೇ ಅಲ್ಲ, ಏಕೆಂದರೆ ಮೂಲ ತತ್ವಗಳು ಮತ್ತು ಪರಿಕಲ್ಪನೆಗಳನ್ನು ಅರ್ಥಮಾಡಿಕೊಳ್ಳದೆ, ಜ್ಞಾನವನ್ನು ಆಳವಾಗಿಸಲು ಸಾಧ್ಯವಾಗುವುದಿಲ್ಲ.
ಇದೇ ರೀತಿಯ ಲೇಖನಗಳು: