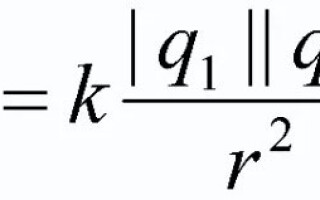ಕೂಲಂಬ್‌ನ ಕಾನೂನು, ವ್ಯಾಖ್ಯಾನ ಮತ್ತು ಸೂತ್ರ - ಎಲೆಕ್ಟ್ರಿಕ್ ಪಾಯಿಂಟ್ ಶುಲ್ಕಗಳು ಮತ್ತು ಅವುಗಳ ಪರಸ್ಪರ ಕ್ರಿಯೆ

ಚಾರ್ಜ್ಡ್ ದೇಹಗಳ ನಡುವೆ ಪರಸ್ಪರ ಕ್ರಿಯೆಯ ಬಲವಿದೆ, ಇದರಿಂದಾಗಿ ಅವರು ಪರಸ್ಪರ ಆಕರ್ಷಿಸಬಹುದು ಅಥವಾ ಹಿಮ್ಮೆಟ್ಟಿಸಬಹುದು. ಕೂಲಂಬ್ನ ಕಾನೂನು ಈ ಬಲವನ್ನು ವಿವರಿಸುತ್ತದೆ, ದೇಹದ ಗಾತ್ರ ಮತ್ತು ಆಕಾರವನ್ನು ಅವಲಂಬಿಸಿ ಅದರ ಕ್ರಿಯೆಯ ಮಟ್ಟವನ್ನು ತೋರಿಸುತ್ತದೆ. ಈ ಭೌತಿಕ ಕಾನೂನನ್ನು ಈ ಲೇಖನದಲ್ಲಿ ಚರ್ಚಿಸಲಾಗುವುದು.

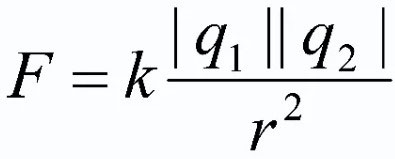
ಕೂಲಂಬ್ ಕಾನೂನು ಸೂತ್ರ.

ವಿಷಯ

1 ಸ್ಟೇಷನರಿ ಪಾಯಿಂಟ್ ಶುಲ್ಕಗಳು
2 ಚಾರ್ಲ್ಸ್ ಕೂಲಂಬ್ನ ತಿರುಚಿದ ಸಮತೋಲನ
3 ಅನುಪಾತದ ಅಂಶ k ಮತ್ತು ವಿದ್ಯುತ್ ಸ್ಥಿರ
4 ಕೂಲಂಬ್ ಬಲದ ದಿಕ್ಕು ಮತ್ತು ಸೂತ್ರದ ವೆಕ್ಟರ್ ರೂಪ
5 ಅಲ್ಲಿ ಕೂಲಂಬ್‌ನ ಕಾನೂನನ್ನು ಆಚರಣೆಯಲ್ಲಿ ಅನ್ವಯಿಸಲಾಗುತ್ತದೆ
6 ಕೂಲಂಬ್ಸ್ ಕಾನೂನಿನಲ್ಲಿ ಬಲಗಳ ನಿರ್ದೇಶನ
7 ಕಾನೂನಿನ ಆವಿಷ್ಕಾರದ ಇತಿಹಾಸ

ಸ್ಟೇಷನರಿ ಪಾಯಿಂಟ್ ಶುಲ್ಕಗಳು

ಕೂಲಂಬ್‌ನ ನಿಯಮವು ಇತರ ವಸ್ತುಗಳಿಂದ ದೂರಕ್ಕಿಂತ ಚಿಕ್ಕದಾಗಿರುವ ಸ್ಥಾಯಿ ಕಾಯಗಳಿಗೆ ಅನ್ವಯಿಸುತ್ತದೆ. ಒಂದು ಬಿಂದು ವಿದ್ಯುತ್ ಚಾರ್ಜ್ ಅಂತಹ ದೇಹಗಳ ಮೇಲೆ ಕೇಂದ್ರೀಕೃತವಾಗಿರುತ್ತದೆ. ದೈಹಿಕ ಸಮಸ್ಯೆಗಳನ್ನು ಪರಿಹರಿಸುವಾಗ, ಪರಿಗಣಿಸಲಾದ ದೇಹಗಳ ಆಯಾಮಗಳನ್ನು ನಿರ್ಲಕ್ಷಿಸಲಾಗುತ್ತದೆ, ಏಕೆಂದರೆ ಅವರು ನಿಜವಾಗಿಯೂ ಪರವಾಗಿಲ್ಲ.

ಪ್ರಾಯೋಗಿಕವಾಗಿ, ವಿಶ್ರಾಂತಿ ಸಮಯದಲ್ಲಿ ಪಾಯಿಂಟ್ ಶುಲ್ಕಗಳನ್ನು ಈ ಕೆಳಗಿನಂತೆ ಚಿತ್ರಿಸಲಾಗಿದೆ:

ಪಾಯಿಂಟ್ ಧನಾತ್ಮಕ ಚಾರ್ಜ್ಡ್ ಚಾರ್ಜ್ q1.

ಈ ಸಂದರ್ಭದಲ್ಲಿ ಪ್ರ₁ ಮತ್ತು ಕ್ಯೂ₂ - ಇದು ಧನಾತ್ಮಕ ವಿದ್ಯುತ್ ಶುಲ್ಕಗಳು, ಮತ್ತು ಕೂಲಂಬ್ ಬಲವು ಅವುಗಳ ಮೇಲೆ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ (ಚಿತ್ರದಲ್ಲಿ ತೋರಿಸಲಾಗಿಲ್ಲ). ಪಾಯಿಂಟ್ ವೈಶಿಷ್ಟ್ಯಗಳ ಗಾತ್ರವು ಅಪ್ರಸ್ತುತವಾಗುತ್ತದೆ.

ಸೂಚನೆ! ವಿಶ್ರಾಂತಿಯಲ್ಲಿರುವ ಶುಲ್ಕಗಳು ಪರಸ್ಪರ ನೀಡಿದ ದೂರದಲ್ಲಿವೆ, ಸಮಸ್ಯೆಗಳಲ್ಲಿ ಇದನ್ನು ಸಾಮಾನ್ಯವಾಗಿ ಆರ್ ಅಕ್ಷರದಿಂದ ಸೂಚಿಸಲಾಗುತ್ತದೆ. ಲೇಖನದಲ್ಲಿ ಮತ್ತಷ್ಟು, ಈ ಶುಲ್ಕಗಳನ್ನು ನಿರ್ವಾತದಲ್ಲಿ ಪರಿಗಣಿಸಲಾಗುತ್ತದೆ.

ಚಾರ್ಲ್ಸ್ ಕೂಲಂಬ್ನ ತಿರುಚಿದ ಸಮತೋಲನ

1777 ರಲ್ಲಿ ಕೂಲಂಬ್ ಅಭಿವೃದ್ಧಿಪಡಿಸಿದ ಈ ಸಾಧನವು ನಂತರ ಅವನ ಹೆಸರಿನ ಶಕ್ತಿಯ ಅವಲಂಬನೆಯನ್ನು ನಿರ್ಣಯಿಸಲು ಸಹಾಯ ಮಾಡಿತು. ಅದರ ಸಹಾಯದಿಂದ, ಪಾಯಿಂಟ್ ಶುಲ್ಕಗಳು, ಹಾಗೆಯೇ ಕಾಂತೀಯ ಧ್ರುವಗಳ ಪರಸ್ಪರ ಕ್ರಿಯೆಯನ್ನು ಅಧ್ಯಯನ ಮಾಡಲಾಗುತ್ತದೆ.

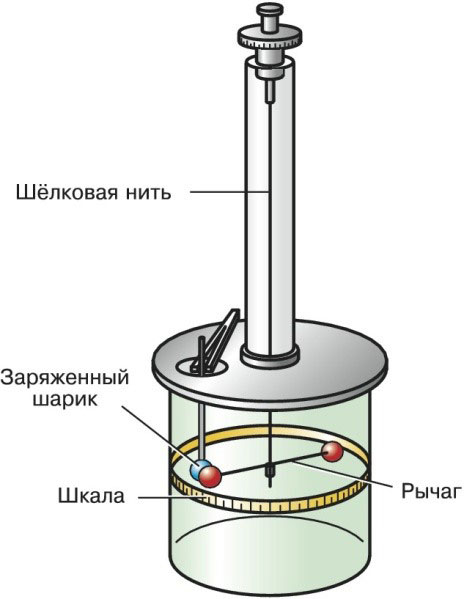
ತಿರುಚಿದ ಸಮತೋಲನವು ಲಂಬವಾದ ಸಮತಲದಲ್ಲಿ ಸಣ್ಣ ರೇಷ್ಮೆ ದಾರವನ್ನು ಹೊಂದಿದೆ, ಇದರಿಂದ ಸಮತೋಲಿತ ಲಿವರ್ ಸ್ಥಗಿತಗೊಳ್ಳುತ್ತದೆ. ಪಾಯಿಂಟ್ ಶುಲ್ಕಗಳು ಲಿವರ್ನ ತುದಿಗಳಲ್ಲಿವೆ.

ಬಾಹ್ಯ ಶಕ್ತಿಗಳ ಕ್ರಿಯೆಯ ಅಡಿಯಲ್ಲಿ, ಲಿವರ್ ಅಡ್ಡಲಾಗಿ ಚಲಿಸಲು ಪ್ರಾರಂಭಿಸುತ್ತದೆ. ಥ್ರೆಡ್ನ ಸ್ಥಿತಿಸ್ಥಾಪಕ ಬಲದಿಂದ ಸಮತೋಲನಗೊಳ್ಳುವವರೆಗೆ ಲಿವರ್ ಸಮತಲದಲ್ಲಿ ಚಲಿಸುತ್ತದೆ.

ಚಲನೆಯ ಪ್ರಕ್ರಿಯೆಯಲ್ಲಿ, ಲಿವರ್ ಲಂಬ ಅಕ್ಷದಿಂದ ಒಂದು ನಿರ್ದಿಷ್ಟ ಕೋನದಿಂದ ವಿಪಥಗೊಳ್ಳುತ್ತದೆ. ಇದನ್ನು d ಎಂದು ತೆಗೆದುಕೊಳ್ಳಲಾಗುತ್ತದೆ ಮತ್ತು ಇದನ್ನು ತಿರುಗುವಿಕೆಯ ಕೋನ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಈ ನಿಯತಾಂಕದ ಮೌಲ್ಯವನ್ನು ತಿಳಿದುಕೊಳ್ಳುವುದು, ಉದ್ಭವಿಸುವ ಶಕ್ತಿಗಳ ಟಾರ್ಕ್ ಅನ್ನು ಕಂಡುಹಿಡಿಯುವುದು ಸಾಧ್ಯ.

ಇದನ್ನೂ ಓದಿ: ಸರಳ ಪದಗಳಲ್ಲಿ ವಿದ್ಯುತ್ ಪ್ರವಾಹ ಎಂದರೇನು

ಚಾರ್ಲ್ಸ್ ಕೂಲಂಬ್ನ ತಿರುಚಿದ ಸಮತೋಲನವು ಈ ರೀತಿ ಕಾಣುತ್ತದೆ:

ಚಾರ್ಲ್ಸ್ ಕೂಲಂಬ್ನ ತಿರುಚಿದ ಸಮತೋಲನ.

ಅನುಪಾತದ ಅಂಶ k ಮತ್ತು ವಿದ್ಯುತ್ ಸ್ಥಿರ 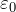$\varepsilon_0$

ಕೂಲಂಬ್ಸ್ ಕಾನೂನಿನ ಸೂತ್ರದಲ್ಲಿ k ನಿಯತಾಂಕಗಳಿವೆ - ಅನುಪಾತದ ಗುಣಾಂಕ ಅಥವಾ $\varepsilon_0$ ವಿದ್ಯುತ್ ಸ್ಥಿರವಾಗಿರುತ್ತದೆ. ವಿದ್ಯುತ್ ಸ್ಥಿರ $\varepsilon_0$ ಅನೇಕ ಉಲ್ಲೇಖ ಪುಸ್ತಕಗಳು, ಪಠ್ಯಪುಸ್ತಕಗಳು, ಇಂಟರ್ನೆಟ್ನಲ್ಲಿ ಪ್ರಸ್ತುತಪಡಿಸಲಾಗಿದೆ ಮತ್ತು ಅದನ್ನು ಎಣಿಸುವ ಅಗತ್ಯವಿಲ್ಲ! ನಿರ್ವಾತ ಅನುಪಾತದ ಅಂಶವನ್ನು ಆಧರಿಸಿದೆ $\varepsilon_0$ ಪ್ರಸಿದ್ಧ ಸೂತ್ರದಿಂದ ಕಂಡುಹಿಡಿಯಬಹುದು:

$k = \frac {1}{4\cdot \pi\cdot \varepsilon_0}$

ಇಲ್ಲಿ $\varepsilon_0=8.85\cdot 10^{-12} \frac {C^2}{H\cdot m^2}$ ವಿದ್ಯುತ್ ಸ್ಥಿರವಾಗಿರುತ್ತದೆ,

$\pi=3.14$ - ಪೈ,

$k=9\cdot 10^{9} \frac {H\cdot m^2}{C^2}$ ನಿರ್ವಾತದಲ್ಲಿ ಅನುಪಾತದ ಗುಣಾಂಕವಾಗಿದೆ.

ಹೆಚ್ಚುವರಿ ಮಾಹಿತಿ! ಮೇಲೆ ಪ್ರಸ್ತುತಪಡಿಸಲಾದ ನಿಯತಾಂಕಗಳನ್ನು ತಿಳಿಯದೆ, ಎರಡು ಪಾಯಿಂಟ್ ಎಲೆಕ್ಟ್ರಿಕ್ ಚಾರ್ಜ್ಗಳ ನಡುವಿನ ಪರಸ್ಪರ ಕ್ರಿಯೆಯ ಬಲವನ್ನು ಕಂಡುಹಿಡಿಯಲು ಇದು ಕಾರ್ಯನಿರ್ವಹಿಸುವುದಿಲ್ಲ.
ಕೂಲಂಬ್ಸ್ ಕಾನೂನಿನ ಸೂತ್ರೀಕರಣ ಮತ್ತು ಸೂತ್ರ

ಮೇಲಿನದನ್ನು ಸಂಕ್ಷಿಪ್ತವಾಗಿ ಹೇಳಲು, ಎಲೆಕ್ಟ್ರೋಸ್ಟಾಟಿಕ್ಸ್ನ ಮುಖ್ಯ ಕಾನೂನಿನ ಅಧಿಕೃತ ಸೂತ್ರೀಕರಣವನ್ನು ನೀಡುವುದು ಅವಶ್ಯಕ. ಇದು ರೂಪವನ್ನು ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ:

ನಿರ್ವಾತದಲ್ಲಿ ಉಳಿದಿರುವ ಎರಡು ಪಾಯಿಂಟ್ ಚಾರ್ಜ್‌ಗಳ ಪರಸ್ಪರ ಕ್ರಿಯೆಯ ಬಲವು ಈ ಚಾರ್ಜ್‌ಗಳ ಉತ್ಪನ್ನಕ್ಕೆ ನೇರವಾಗಿ ಅನುಪಾತದಲ್ಲಿರುತ್ತದೆ ಮತ್ತು ಅವುಗಳ ನಡುವಿನ ಅಂತರದ ವರ್ಗಕ್ಕೆ ವಿಲೋಮ ಅನುಪಾತದಲ್ಲಿರುತ್ತದೆ. ಇದಲ್ಲದೆ, ಶುಲ್ಕಗಳ ಉತ್ಪನ್ನವನ್ನು ಮಾಡ್ಯೂಲೋ ತೆಗೆದುಕೊಳ್ಳಬೇಕು!

$F=k\cdot \frac {|q_1|\cdot |q_2|}{r^2}$

ಈ ಸೂತ್ರದಲ್ಲಿ ಕ್ಯೂ₁ ಮತ್ತು ಕ್ಯೂ₂ಪಾಯಿಂಟ್ ಶುಲ್ಕಗಳು, ದೇಹಗಳನ್ನು ಪರಿಗಣಿಸಲಾಗಿದೆ; ಆರ್² - ಚೌಕದಲ್ಲಿ ತೆಗೆದುಕೊಂಡ ಈ ದೇಹಗಳ ನಡುವಿನ ಸಮತಲದ ಅಂತರ; k ಎಂಬುದು ಅನುಪಾತದ ಗುಣಾಂಕವಾಗಿದೆ ( $9\cdot 10^{9} \frac {H\cdot m^2}{C^2}$ ನಿರ್ವಾತಕ್ಕಾಗಿ).

ಕೂಲಂಬ್ ಬಲದ ದಿಕ್ಕು ಮತ್ತು ಸೂತ್ರದ ವೆಕ್ಟರ್ ರೂಪ

ಸೂತ್ರದ ಸಂಪೂರ್ಣ ತಿಳುವಳಿಕೆಗಾಗಿ, ಕೂಲಂಬ್ನ ಕಾನೂನನ್ನು ದೃಶ್ಯೀಕರಿಸಬಹುದು:

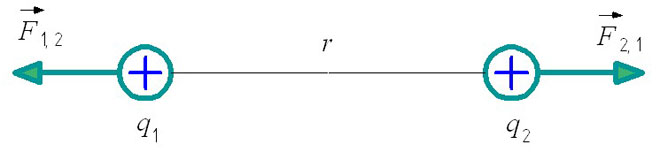
ಒಂದೇ ಧ್ರುವೀಯತೆಯ ಎರಡು ಪಾಯಿಂಟ್ ಚಾರ್ಜ್‌ಗಳಿಗೆ ಕೂಲಂಬ್ ಬಲದ ನಿರ್ದೇಶನ.

ಎಫ್_1,2- ಎರಡನೆಯದಕ್ಕೆ ಸಂಬಂಧಿಸಿದಂತೆ ಮೊದಲ ಚಾರ್ಜ್ನ ಪರಸ್ಪರ ಕ್ರಿಯೆಯ ಬಲ.

ಎಫ್_2,1- ಮೊದಲನೆಯದಕ್ಕೆ ಸಂಬಂಧಿಸಿದಂತೆ ಎರಡನೇ ಚಾರ್ಜ್ನ ಪರಸ್ಪರ ಕ್ರಿಯೆಯ ಬಲ.

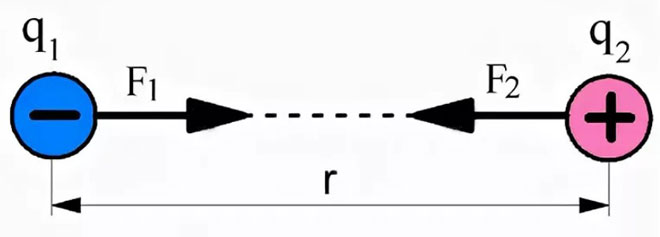
ಅಲ್ಲದೆ, ಸ್ಥಾಯೀವಿದ್ಯುತ್ತಿನ ಸಮಸ್ಯೆಗಳನ್ನು ಪರಿಹರಿಸುವಾಗ, ಒಂದು ಪ್ರಮುಖ ನಿಯಮವನ್ನು ಗಣನೆಗೆ ತೆಗೆದುಕೊಳ್ಳುವುದು ಅವಶ್ಯಕ: ಅದೇ ಹೆಸರಿನ ವಿದ್ಯುತ್ ಶುಲ್ಕಗಳು ಹಿಮ್ಮೆಟ್ಟಿಸುತ್ತದೆ ಮತ್ತು ವಿರುದ್ಧವಾದ ಶುಲ್ಕಗಳು ಆಕರ್ಷಿಸುತ್ತವೆ. ಚಿತ್ರದಲ್ಲಿನ ಪರಸ್ಪರ ಶಕ್ತಿಗಳ ಸ್ಥಳವು ಇದನ್ನು ಅವಲಂಬಿಸಿರುತ್ತದೆ.

ವಿರುದ್ಧ ಆರೋಪಗಳನ್ನು ಪರಿಗಣಿಸಿದರೆ, ಅವರ ಪರಸ್ಪರ ಕ್ರಿಯೆಯ ಶಕ್ತಿಗಳು ಪರಸ್ಪರ ಕಡೆಗೆ ನಿರ್ದೇಶಿಸಲ್ಪಡುತ್ತವೆ, ಅವುಗಳ ಆಕರ್ಷಣೆಯನ್ನು ಚಿತ್ರಿಸುತ್ತವೆ.

ವಿಭಿನ್ನ ಧ್ರುವೀಯತೆಯ ಎರಡು ಪಾಯಿಂಟ್ ಚಾರ್ಜ್‌ಗಳಿಗೆ ಕೂಲಂಬ್ ಫೋರ್ಸ್‌ನ ನಿರ್ದೇಶನ.

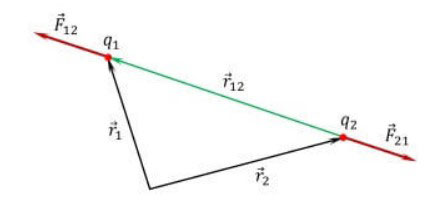
ವೆಕ್ಟರ್ ರೂಪದಲ್ಲಿ ಸ್ಥಾಯೀವಿದ್ಯುತ್ತಿನ ಮೂಲ ನಿಯಮದ ಸೂತ್ರವನ್ನು ಈ ಕೆಳಗಿನಂತೆ ಪ್ರತಿನಿಧಿಸಬಹುದು:

$\vec F_1_2=\frac {1}{4\cdot \pi\cdot \varepsilon_0}\cdot \frac {q_1\cdot q_2}{r_1_2^3}\cdot \vec r_1_2$

$\vec F_1_2$ ಚಾರ್ಜ್ q2 ನ ಬದಿಯಿಂದ ಪಾಯಿಂಟ್ ಚಾರ್ಜ್ q1 ಮೇಲೆ ಕಾರ್ಯನಿರ್ವಹಿಸುವ ಬಲವಾಗಿದೆ,

$\vec r_1_2$ ಚಾರ್ಜ್ q2 ಅನ್ನು ಚಾರ್ಜ್ q1 ನೊಂದಿಗೆ ಸಂಪರ್ಕಿಸುವ ತ್ರಿಜ್ಯದ ವೆಕ್ಟರ್ ಆಗಿದೆ,

ಇದನ್ನೂ ಓದಿ: ಮನೆಯಲ್ಲಿ ಎಲೆಕ್ಟ್ರಾನಿಕ್ ಪ್ರಿಂಟೆಡ್ ಸರ್ಕ್ಯೂಟ್ ಬೋರ್ಡ್ ಅನ್ನು ಹೇಗೆ ತಯಾರಿಸುವುದು?

$r=|\vec r_1_2|$

ಪ್ರಮುಖ! ಸೂತ್ರವನ್ನು ವೆಕ್ಟರ್ ರೂಪದಲ್ಲಿ ಬರೆದ ನಂತರ, ಚಿಹ್ನೆಗಳನ್ನು ಸರಿಯಾಗಿ ಹಾಕಲು ಎರಡು ಪಾಯಿಂಟ್ ಎಲೆಕ್ಟ್ರಿಕ್ ಚಾರ್ಜ್‌ಗಳ ಸಂವಾದಾತ್ಮಕ ಶಕ್ತಿಗಳನ್ನು ಅಕ್ಷದ ಮೇಲೆ ಪ್ರಕ್ಷೇಪಿಸಬೇಕಾಗುತ್ತದೆ. ಈ ಕ್ರಿಯೆಯು ಔಪಚಾರಿಕತೆಯಾಗಿದೆ ಮತ್ತು ಯಾವುದೇ ಟಿಪ್ಪಣಿಗಳಿಲ್ಲದೆ ಮಾನಸಿಕವಾಗಿ ನಿರ್ವಹಿಸಲಾಗುತ್ತದೆ.

ಅಲ್ಲಿ ಕೂಲಂಬ್‌ನ ಕಾನೂನನ್ನು ಆಚರಣೆಯಲ್ಲಿ ಅನ್ವಯಿಸಲಾಗುತ್ತದೆ

ಸ್ಥಾಯೀವಿದ್ಯುತ್ತಿನ ಮೂಲ ನಿಯಮವು ಚಾರ್ಲ್ಸ್ ಕೂಲಂಬ್ನ ಪ್ರಮುಖ ಆವಿಷ್ಕಾರವಾಗಿದೆ, ಇದು ಅನೇಕ ಪ್ರದೇಶಗಳಲ್ಲಿ ತನ್ನ ಅನ್ವಯವನ್ನು ಕಂಡುಕೊಂಡಿದೆ.

ಪ್ರಸಿದ್ಧ ಭೌತಶಾಸ್ತ್ರಜ್ಞರ ಕೃತಿಗಳನ್ನು ವಿವಿಧ ಸಾಧನಗಳು, ಸಾಧನಗಳು, ಉಪಕರಣಗಳನ್ನು ಆವಿಷ್ಕರಿಸುವ ಪ್ರಕ್ರಿಯೆಯಲ್ಲಿ ಬಳಸಲಾಯಿತು. ಉದಾಹರಣೆಗೆ, ಮಿಂಚಿನ ರಾಡ್.

ಮಿಂಚಿನ ರಾಡ್ ಸಹಾಯದಿಂದ, ವಸತಿ ಕಟ್ಟಡಗಳು ಮತ್ತು ಕಟ್ಟಡಗಳು ಗುಡುಗು ಸಹಿತ ಮಿಂಚಿನಿಂದ ರಕ್ಷಿಸಲ್ಪಡುತ್ತವೆ. ಹೀಗಾಗಿ, ವಿದ್ಯುತ್ ಉಪಕರಣಗಳ ರಕ್ಷಣೆಯ ಮಟ್ಟವು ಹೆಚ್ಚಾಗುತ್ತದೆ.

ಮಿಂಚಿನ ರಾಡ್ ಈ ಕೆಳಗಿನ ತತ್ತ್ವದ ಪ್ರಕಾರ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ: ಗುಡುಗು ಸಹಿತ, ಬಲವಾದ ಇಂಡಕ್ಷನ್ ಶುಲ್ಕಗಳು ಕ್ರಮೇಣ ನೆಲದ ಮೇಲೆ ಸಂಗ್ರಹಗೊಳ್ಳಲು ಪ್ರಾರಂಭಿಸುತ್ತವೆ, ಅದು ಮೇಲೇರುತ್ತದೆ ಮತ್ತು ಮೋಡಗಳಿಗೆ ಆಕರ್ಷಿತವಾಗುತ್ತದೆ. ಈ ಸಂದರ್ಭದಲ್ಲಿ, ನೆಲದ ಮೇಲೆ ದೊಡ್ಡ ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರವು ರೂಪುಗೊಳ್ಳುತ್ತದೆ. ಮಿಂಚಿನ ರಾಡ್ ಬಳಿ, ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರವು ಬಲಗೊಳ್ಳುತ್ತದೆ, ಇದರಿಂದಾಗಿ ಸಾಧನದ ತುದಿಯಿಂದ ಕರೋನಾ ವಿದ್ಯುದಾವೇಶವನ್ನು ಹೊತ್ತಿಕೊಳ್ಳಲಾಗುತ್ತದೆ.

ಇದಲ್ಲದೆ, ನೆಲದ ಮೇಲೆ ರೂಪುಗೊಂಡ ಚಾರ್ಜ್ ವಿರುದ್ಧ ಚಿಹ್ನೆಯೊಂದಿಗೆ ಮೋಡದ ಚಾರ್ಜ್‌ಗೆ ಆಕರ್ಷಿತವಾಗಲು ಪ್ರಾರಂಭಿಸುತ್ತದೆ, ಏಕೆಂದರೆ ಅದು ಚಾರ್ಲ್ಸ್ ಕೂಲಂಬ್‌ನ ಕಾನೂನಿನ ಪ್ರಕಾರ ಇರಬೇಕು. ಅದರ ನಂತರ, ಗಾಳಿಯು ಅಯಾನೀಕರಣದ ಪ್ರಕ್ರಿಯೆಯ ಮೂಲಕ ಹೋಗುತ್ತದೆ, ಮತ್ತು ಮಿಂಚಿನ ರಾಡ್ನ ಕೊನೆಯಲ್ಲಿ ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರದ ಶಕ್ತಿಯು ಕಡಿಮೆಯಾಗುತ್ತದೆ. ಹೀಗಾಗಿ, ಮಿಂಚು ಕಟ್ಟಡಕ್ಕೆ ಪ್ರವೇಶಿಸುವ ಅಪಾಯ ಕಡಿಮೆಯಾಗಿದೆ.

ಸೂಚನೆ! ಮಿಂಚಿನ ರಾಡ್ ಅನ್ನು ಸ್ಥಾಪಿಸಿದ ಕಟ್ಟಡವನ್ನು ಹೊಡೆದರೆ, ನಂತರ ಬೆಂಕಿ ಇರುವುದಿಲ್ಲ, ಮತ್ತು ಎಲ್ಲಾ ಶಕ್ತಿಯು ನೆಲಕ್ಕೆ ಹೋಗುತ್ತದೆ.

ಕೂಲಂಬ್ಸ್ ನಿಯಮವನ್ನು ಆಧರಿಸಿ, "ಪಾರ್ಟಿಕಲ್ ಆಕ್ಸಿಲರೇಟರ್" ಎಂಬ ಸಾಧನವನ್ನು ಅಭಿವೃದ್ಧಿಪಡಿಸಲಾಯಿತು, ಇದು ಇಂದು ಹೆಚ್ಚಿನ ಬೇಡಿಕೆಯಲ್ಲಿದೆ.

ಈ ಸಾಧನದಲ್ಲಿ, ಬಲವಾದ ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರವನ್ನು ರಚಿಸಲಾಗಿದೆ, ಇದು ಅದರೊಳಗೆ ಬೀಳುವ ಕಣಗಳ ಶಕ್ತಿಯನ್ನು ಹೆಚ್ಚಿಸುತ್ತದೆ.

ಕೂಲಂಬ್ಸ್ ಕಾನೂನಿನಲ್ಲಿ ಬಲಗಳ ನಿರ್ದೇಶನ

ಮೇಲೆ ಹೇಳಿದಂತೆ, ಎರಡು ಪಾಯಿಂಟ್ ಎಲೆಕ್ಟ್ರಿಕ್ ಚಾರ್ಜ್‌ಗಳ ಪರಸ್ಪರ ಕ್ರಿಯೆಯ ದಿಕ್ಕು ಅವುಗಳ ಧ್ರುವೀಯತೆಯನ್ನು ಅವಲಂಬಿಸಿರುತ್ತದೆ. ಆ. ಅದೇ ಹೆಸರಿನ ಆರೋಪಗಳು ಹಿಮ್ಮೆಟ್ಟಿಸುತ್ತವೆ ಮತ್ತು ವಿರುದ್ಧ ಶುಲ್ಕಗಳ ಶುಲ್ಕಗಳು ಆಕರ್ಷಿಸುತ್ತವೆ.

ಇದನ್ನೂ ಓದಿ: ನಿಮ್ಮ ಸ್ವಂತ ಕೈಗಳಿಂದ ಮೆಟಲ್ ಡಿಟೆಕ್ಟರ್ ಅನ್ನು ಹೇಗೆ ತಯಾರಿಸುವುದು, ಆರಂಭಿಕರಿಗಾಗಿ ಸಹಾಯ

ಕೂಲಂಬ್ ಬಲಗಳನ್ನು ತ್ರಿಜ್ಯ ವೆಕ್ಟರ್ ಎಂದೂ ಕರೆಯಬಹುದು, ಏಕೆಂದರೆ ಅವುಗಳನ್ನು ಅವುಗಳ ನಡುವೆ ಎಳೆಯುವ ರೇಖೆಯ ಉದ್ದಕ್ಕೂ ನಿರ್ದೇಶಿಸಲಾಗುತ್ತದೆ.

ಕೆಲವು ದೈಹಿಕ ಸಮಸ್ಯೆಗಳಲ್ಲಿ, ಸಂಕೀರ್ಣ ಆಕಾರದ ದೇಹಗಳನ್ನು ನೀಡಲಾಗುತ್ತದೆ, ಇದು ಪಾಯಿಂಟ್ ಎಲೆಕ್ಟ್ರಿಕ್ ಚಾರ್ಜ್ಗಾಗಿ ತೆಗೆದುಕೊಳ್ಳಲಾಗುವುದಿಲ್ಲ, ಅಂದರೆ. ಅದರ ಗಾತ್ರವನ್ನು ನಿರ್ಲಕ್ಷಿಸಿ. ಈ ಪರಿಸ್ಥಿತಿಯಲ್ಲಿ, ಪರಿಗಣನೆಯಲ್ಲಿರುವ ದೇಹವನ್ನು ಹಲವಾರು ಸಣ್ಣ ಭಾಗಗಳಾಗಿ ವಿಂಗಡಿಸಬೇಕು ಮತ್ತು ಪ್ರತಿ ಭಾಗವನ್ನು ಪ್ರತ್ಯೇಕವಾಗಿ ಲೆಕ್ಕ ಹಾಕಬೇಕು, ಕೂಲಂಬ್ಸ್ ಕಾನೂನನ್ನು ಬಳಸಿ.

ವಿಭಜಿಸುವ ಮೂಲಕ ಪಡೆದ ಬಲ ವಾಹಕಗಳನ್ನು ಬೀಜಗಣಿತ ಮತ್ತು ರೇಖಾಗಣಿತದ ನಿಯಮಗಳ ಪ್ರಕಾರ ಸಂಕ್ಷೇಪಿಸಲಾಗಿದೆ. ಫಲಿತಾಂಶವು ಫಲಿತಾಂಶದ ಬಲವಾಗಿದೆ, ಇದು ಈ ಸಮಸ್ಯೆಗೆ ಉತ್ತರವಾಗಿರುತ್ತದೆ. ಈ ಪರಿಹಾರ ವಿಧಾನವನ್ನು ಸಾಮಾನ್ಯವಾಗಿ ತ್ರಿಕೋನ ವಿಧಾನ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

ಕೂಲಂಬ್ ಫೋರ್ಸ್ ವೆಕ್ಟರ್‌ಗಳ ದಿಕ್ಕು.

ಕಾನೂನಿನ ಆವಿಷ್ಕಾರದ ಇತಿಹಾಸ

ಮೇಲೆ ಪರಿಗಣಿಸಲಾದ ಕಾನೂನಿನ ಮೂಲಕ ಎರಡು ಪಾಯಿಂಟ್ ಆರೋಪಗಳ ಪರಸ್ಪರ ಕ್ರಿಯೆಗಳನ್ನು ಮೊದಲು 1785 ರಲ್ಲಿ ಚಾರ್ಲ್ಸ್ ಕೂಲಂಬ್ ಸಾಬೀತುಪಡಿಸಿದರು. ಭೌತಶಾಸ್ತ್ರಜ್ಞರು ತಿರುಚುವ ಸಮತೋಲನಗಳನ್ನು ಬಳಸಿಕೊಂಡು ರೂಪಿಸಿದ ಕಾನೂನಿನ ನಿಖರತೆಯನ್ನು ಸಾಬೀತುಪಡಿಸುವಲ್ಲಿ ಯಶಸ್ವಿಯಾದರು, ಅದರ ಕಾರ್ಯಾಚರಣೆಯ ತತ್ವವನ್ನು ಸಹ ಲೇಖನದಲ್ಲಿ ಪ್ರಸ್ತುತಪಡಿಸಲಾಗಿದೆ.

ಗೋಳಾಕಾರದ ಕೆಪಾಸಿಟರ್ ಒಳಗೆ ಯಾವುದೇ ವಿದ್ಯುದಾವೇಶವಿಲ್ಲ ಎಂದು ಕೂಲಂಬ್ ಸಾಬೀತುಪಡಿಸಿದರು. ಆದ್ದರಿಂದ ಪರಿಗಣನೆಯಲ್ಲಿರುವ ದೇಹಗಳ ನಡುವಿನ ಅಂತರವನ್ನು ಬದಲಾಯಿಸುವ ಮೂಲಕ ಸ್ಥಾಯೀವಿದ್ಯುತ್ತಿನ ಶಕ್ತಿಗಳ ಪ್ರಮಾಣವನ್ನು ಬದಲಾಯಿಸಬಹುದು ಎಂಬ ಹೇಳಿಕೆಗೆ ಅವರು ಬಂದರು.

ಹೀಗಾಗಿ, ಕೂಲಂಬ್‌ನ ನಿಯಮವು ಇನ್ನೂ ಸ್ಥಾಯೀವಿದ್ಯುತ್ತಿನ ಪ್ರಮುಖ ನಿಯಮವಾಗಿದೆ, ಅದರ ಆಧಾರದ ಮೇಲೆ ಅನೇಕ ಶ್ರೇಷ್ಠ ಆವಿಷ್ಕಾರಗಳನ್ನು ಮಾಡಲಾಗಿದೆ. ಈ ಲೇಖನದ ಚೌಕಟ್ಟಿನೊಳಗೆ, ಕಾನೂನಿನ ಅಧಿಕೃತ ಮಾತುಗಳನ್ನು ಪ್ರಸ್ತುತಪಡಿಸಲಾಗಿದೆ, ಜೊತೆಗೆ ಅದರ ಘಟಕ ಭಾಗಗಳನ್ನು ವಿವರವಾಗಿ ವಿವರಿಸಲಾಗಿದೆ.

ಇದೇ ರೀತಿಯ ಲೇಖನಗಳು: