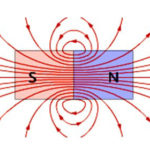
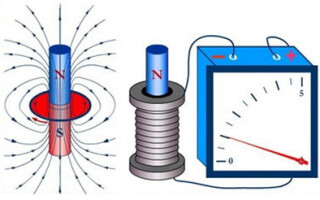
ವಸ್ತುವಿನಲ್ಲಿ, ಅದರ ಸಂಭವಿಸುವ ಸಂದರ್ಭಗಳಲ್ಲಿ ಇಎಮ್ಎಫ್ ಇಂಡಕ್ಷನ್ ಪರಿಕಲ್ಪನೆಯನ್ನು ನಾವು ಅರ್ಥಮಾಡಿಕೊಳ್ಳುತ್ತೇವೆ. ವಾಹಕದಲ್ಲಿ ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರವು ಕಾಣಿಸಿಕೊಂಡಾಗ ಕಾಂತೀಯ ಹರಿವಿನ ಸಂಭವಕ್ಕೆ ನಾವು ಇಂಡಕ್ಟನ್ಸ್ ಅನ್ನು ಪ್ರಮುಖ ನಿಯತಾಂಕವಾಗಿ ಪರಿಗಣಿಸುತ್ತೇವೆ.
ವಿದ್ಯುತ್ಕಾಂತೀಯ ಪ್ರಚೋದನೆಯು ಕಾಲಾನಂತರದಲ್ಲಿ ಬದಲಾಗುವ ಕಾಂತೀಯ ಕ್ಷೇತ್ರಗಳಿಂದ ವಿದ್ಯುತ್ ಪ್ರವಾಹದ ಉತ್ಪಾದನೆಯಾಗಿದೆ. ಫ್ಯಾರಡೆ ಮತ್ತು ಲೆನ್ಜ್ ಅವರ ಆವಿಷ್ಕಾರಗಳಿಗೆ ಧನ್ಯವಾದಗಳು, ಮಾದರಿಗಳನ್ನು ಕಾನೂನುಗಳಾಗಿ ರೂಪಿಸಲಾಯಿತು, ಇದು ವಿದ್ಯುತ್ಕಾಂತೀಯ ಹರಿವಿನ ತಿಳುವಳಿಕೆಗೆ ಸಮ್ಮಿತಿಯನ್ನು ಪರಿಚಯಿಸಿತು. ಮ್ಯಾಕ್ಸ್ವೆಲ್ನ ಸಿದ್ಧಾಂತವು ವಿದ್ಯುತ್ ಪ್ರವಾಹ ಮತ್ತು ಕಾಂತೀಯ ಹರಿವಿನ ಬಗ್ಗೆ ಜ್ಞಾನವನ್ನು ಒಟ್ಟುಗೂಡಿಸಿತು. ಹರ್ಟ್ಜ್ನ ಆವಿಷ್ಕಾರಕ್ಕೆ ಧನ್ಯವಾದಗಳು, ಮಾನವೀಯತೆಯು ದೂರಸಂಪರ್ಕವನ್ನು ಕಲಿತಿದೆ.
ವಿಷಯ
ಕಾಂತೀಯ ಹರಿವು
ವಿದ್ಯುತ್ ಪ್ರವಾಹದೊಂದಿಗೆ ವಾಹಕದ ಸುತ್ತಲೂ ವಿದ್ಯುತ್ಕಾಂತೀಯ ಕ್ಷೇತ್ರವು ಕಾಣಿಸಿಕೊಳ್ಳುತ್ತದೆ, ಆದಾಗ್ಯೂ, ಸಮಾನಾಂತರವಾಗಿ, ವಿರುದ್ಧ ವಿದ್ಯಮಾನವು ಸಹ ಸಂಭವಿಸುತ್ತದೆ - ವಿದ್ಯುತ್ಕಾಂತೀಯ ಇಂಡಕ್ಷನ್.ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಅನ್ನು ಉದಾಹರಣೆಯಾಗಿ ಪರಿಗಣಿಸಿ: ವಾಹಕ ಚೌಕಟ್ಟನ್ನು ಇಂಡಕ್ಷನ್ನೊಂದಿಗೆ ವಿದ್ಯುತ್ ಕ್ಷೇತ್ರದಲ್ಲಿ ಇರಿಸಿದರೆ ಮತ್ತು ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ರೇಖೆಗಳ ಉದ್ದಕ್ಕೂ ಮೇಲಿನಿಂದ ಕೆಳಕ್ಕೆ ಅಥವಾ ಅವುಗಳಿಗೆ ಲಂಬವಾಗಿ ಬಲ ಅಥವಾ ಎಡಕ್ಕೆ ಚಲಿಸಿದರೆ, ಫ್ರೇಮ್ ಮೂಲಕ ಹಾದುಹೋಗುವ ಕಾಂತೀಯ ಹರಿವು ನಿರಂತರ.
ಫ್ರೇಮ್ ಅದರ ಅಕ್ಷದ ಸುತ್ತ ತಿರುಗಿದಾಗ, ಸ್ವಲ್ಪ ಸಮಯದ ನಂತರ ಕಾಂತೀಯ ಹರಿವು ನಿರ್ದಿಷ್ಟ ಪ್ರಮಾಣದಲ್ಲಿ ಬದಲಾಗುತ್ತದೆ. ಪರಿಣಾಮವಾಗಿ, ಇಂಡಕ್ಷನ್ನ ಇಎಮ್ಎಫ್ ಫ್ರೇಮ್ನಲ್ಲಿ ಕಾಣಿಸಿಕೊಳ್ಳುತ್ತದೆ ಮತ್ತು ವಿದ್ಯುತ್ ಪ್ರವಾಹವು ಕಾಣಿಸಿಕೊಳ್ಳುತ್ತದೆ, ಇದನ್ನು ಇಂಡಕ್ಷನ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.
ಇಎಮ್ಎಫ್ ಇಂಡಕ್ಷನ್
ಇಂಡಕ್ಷನ್ನ ಇಎಮ್ಎಫ್ನ ಪರಿಕಲ್ಪನೆಯು ಏನೆಂದು ನಾವು ವಿವರವಾಗಿ ಪರಿಶೀಲಿಸೋಣ. ವಾಹಕವನ್ನು ಆಯಸ್ಕಾಂತೀಯ ಕ್ಷೇತ್ರದಲ್ಲಿ ಇರಿಸಿದಾಗ ಮತ್ತು ಅದು ಕ್ಷೇತ್ರ ರೇಖೆಗಳ ಛೇದಕದೊಂದಿಗೆ ಚಲಿಸಿದಾಗ, ಇಂಡಕ್ಷನ್ ಇಎಮ್ಎಫ್ ಎಂಬ ವಾಹಕದಲ್ಲಿ ಎಲೆಕ್ಟ್ರೋಮೋಟಿವ್ ಫೋರ್ಸ್ ಕಾಣಿಸಿಕೊಳ್ಳುತ್ತದೆ. ವಾಹಕವು ಸ್ಥಿರವಾಗಿ ಉಳಿದಿದ್ದರೆ ಮತ್ತು ಕಾಂತೀಯ ಕ್ಷೇತ್ರವು ಬಲದ ವಾಹಕದ ರೇಖೆಗಳೊಂದಿಗೆ ಚಲಿಸುತ್ತದೆ ಮತ್ತು ಛೇದಿಸಿದರೆ ಇದು ಸಂಭವಿಸುತ್ತದೆ.
ಕಂಡಕ್ಟರ್, ಅಲ್ಲಿ ಇಎಮ್ಎಫ್ ಸಂಭವಿಸಿದಾಗ, ಬಾಹ್ಯ ಸರ್ಕ್ಯೂಟ್ಗೆ ಮುಚ್ಚಿದಾಗ, ಈ ಇಎಮ್ಎಫ್ನ ಉಪಸ್ಥಿತಿಯಿಂದಾಗಿ, ಇಂಡಕ್ಷನ್ ಪ್ರವಾಹವು ಸರ್ಕ್ಯೂಟ್ ಮೂಲಕ ಹರಿಯಲು ಪ್ರಾರಂಭವಾಗುತ್ತದೆ. ವಿದ್ಯುತ್ಕಾಂತೀಯ ಪ್ರಚೋದನೆಯು ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ರೇಖೆಗಳಿಂದ ದಾಟಿದ ಕ್ಷಣದಲ್ಲಿ ಕಂಡಕ್ಟರ್ನಲ್ಲಿ ಇಎಮ್ಎಫ್ ಇಂಡಕ್ಷನ್ನ ವಿದ್ಯಮಾನವನ್ನು ಒಳಗೊಂಡಿರುತ್ತದೆ.
ವಿದ್ಯುತ್ಕಾಂತೀಯ ಪ್ರಚೋದನೆಯು ಯಾಂತ್ರಿಕ ಶಕ್ತಿಯನ್ನು ವಿದ್ಯುತ್ ಪ್ರವಾಹವಾಗಿ ಪರಿವರ್ತಿಸುವ ಹಿಮ್ಮುಖ ಪ್ರಕ್ರಿಯೆಯಾಗಿದೆ. ಈ ಪರಿಕಲ್ಪನೆ ಮತ್ತು ಅದರ ಕಾನೂನುಗಳನ್ನು ಎಲೆಕ್ಟ್ರಿಕಲ್ ಎಂಜಿನಿಯರಿಂಗ್ನಲ್ಲಿ ವ್ಯಾಪಕವಾಗಿ ಬಳಸಲಾಗುತ್ತದೆ, ಹೆಚ್ಚಿನ ವಿದ್ಯುತ್ ಯಂತ್ರಗಳು ಈ ವಿದ್ಯಮಾನವನ್ನು ಆಧರಿಸಿವೆ.
ಫ್ಯಾರಡೆ ಮತ್ತು ಲೆನ್ಜ್ ಕಾನೂನುಗಳು
ಫ್ಯಾರಡೆ ಮತ್ತು ಲೆನ್ಜ್ ನಿಯಮಗಳು ವಿದ್ಯುತ್ಕಾಂತೀಯ ಇಂಡಕ್ಷನ್ ಸಂಭವಿಸುವಿಕೆಯ ಮಾದರಿಗಳನ್ನು ಪ್ರತಿಬಿಂಬಿಸುತ್ತವೆ.
ಕಾಲಾನಂತರದಲ್ಲಿ ಕಾಂತೀಯ ಹರಿವಿನ ಬದಲಾವಣೆಗಳ ಪರಿಣಾಮವಾಗಿ ಕಾಂತೀಯ ಪರಿಣಾಮಗಳು ಕಂಡುಬರುತ್ತವೆ ಎಂದು ಫ್ಯಾರಡೆ ಕಂಡುಕೊಂಡರು.ಪರ್ಯಾಯ ಕಾಂತೀಯ ಪ್ರವಾಹದೊಂದಿಗೆ ವಾಹಕವನ್ನು ದಾಟುವ ಕ್ಷಣದಲ್ಲಿ, ಎಲೆಕ್ಟ್ರೋಮೋಟಿವ್ ಫೋರ್ಸ್ ಅದರಲ್ಲಿ ಉದ್ಭವಿಸುತ್ತದೆ, ಇದು ವಿದ್ಯುತ್ ಪ್ರವಾಹದ ನೋಟಕ್ಕೆ ಕಾರಣವಾಗುತ್ತದೆ. ಶಾಶ್ವತ ಮ್ಯಾಗ್ನೆಟ್ ಮತ್ತು ಎಲೆಕ್ಟ್ರೋಮ್ಯಾಗ್ನೆಟ್ ಎರಡೂ ಪ್ರಸ್ತುತವನ್ನು ಉತ್ಪಾದಿಸಬಹುದು.
ಸರ್ಕ್ಯೂಟ್ ಅನ್ನು ದಾಟುವ ಬಲದ ರೇಖೆಗಳ ಸಂಖ್ಯೆಯಲ್ಲಿ ತ್ವರಿತ ಬದಲಾವಣೆಯೊಂದಿಗೆ ಪ್ರವಾಹದ ತೀವ್ರತೆಯು ಹೆಚ್ಚಾಗುತ್ತದೆ ಎಂದು ವಿಜ್ಞಾನಿ ನಿರ್ಧರಿಸಿದರು. ಅಂದರೆ, ವಿದ್ಯುತ್ಕಾಂತೀಯ ಪ್ರಚೋದನೆಯ EMF ಕಾಂತೀಯ ಹರಿವಿನ ವೇಗಕ್ಕೆ ನೇರ ಅನುಪಾತದಲ್ಲಿರುತ್ತದೆ.
ಫ್ಯಾರಡೆಯ ಕಾನೂನಿನ ಪ್ರಕಾರ, ಇಂಡಕ್ಷನ್ ಇಎಮ್ಎಫ್ ಸೂತ್ರಗಳನ್ನು ಈ ಕೆಳಗಿನಂತೆ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ:
ಇ \u003d - dF / dt.
ಮೈನಸ್ ಚಿಹ್ನೆಯು ಪ್ರೇರಿತ EMF ನ ಧ್ರುವೀಯತೆ, ಹರಿವಿನ ದಿಕ್ಕು ಮತ್ತು ಬದಲಾಗುವ ವೇಗದ ನಡುವಿನ ಸಂಬಂಧವನ್ನು ಸೂಚಿಸುತ್ತದೆ.
ಲೆನ್ಜ್ ನಿಯಮದ ಪ್ರಕಾರ, ಅದರ ದಿಕ್ಕನ್ನು ಅವಲಂಬಿಸಿ ಎಲೆಕ್ಟ್ರೋಮೋಟಿವ್ ಬಲವನ್ನು ನಿರೂಪಿಸಲು ಸಾಧ್ಯವಿದೆ. ಸುರುಳಿಯಲ್ಲಿನ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ನಲ್ಲಿನ ಯಾವುದೇ ಬದಲಾವಣೆಯು ಇಂಡಕ್ಷನ್ನ ಇಎಮ್ಎಫ್ನ ನೋಟಕ್ಕೆ ಕಾರಣವಾಗುತ್ತದೆ, ಮತ್ತು ತ್ವರಿತ ಬದಲಾವಣೆಯೊಂದಿಗೆ, ಹೆಚ್ಚುತ್ತಿರುವ ಇಎಮ್ಎಫ್ ಅನ್ನು ಗಮನಿಸಬಹುದು.
ಇಂಡಕ್ಷನ್ನ ಇಎಮ್ಎಫ್ ಇರುವ ಕಾಯಿಲ್ ಬಾಹ್ಯ ಸರ್ಕ್ಯೂಟ್ಗೆ ಶಾರ್ಟ್ ಸರ್ಕ್ಯೂಟ್ ಹೊಂದಿದ್ದರೆ, ಅದರ ಮೂಲಕ ಇಂಡಕ್ಷನ್ ಕರೆಂಟ್ ಹರಿಯುತ್ತದೆ, ಇದರ ಪರಿಣಾಮವಾಗಿ ವಾಹಕದ ಸುತ್ತಲೂ ಕಾಂತೀಯ ಕ್ಷೇತ್ರವು ಕಾಣಿಸಿಕೊಳ್ಳುತ್ತದೆ ಮತ್ತು ಸುರುಳಿಯು ಸೊಲೆನಾಯ್ಡ್ ಗುಣಲಕ್ಷಣಗಳನ್ನು ಪಡೆಯುತ್ತದೆ. . ಪರಿಣಾಮವಾಗಿ, ಸುರುಳಿಯ ಸುತ್ತಲೂ ಕಾಂತೀಯ ಕ್ಷೇತ್ರವು ರೂಪುಗೊಳ್ಳುತ್ತದೆ.
E.Kh. ಲೆನ್ಜ್ ಒಂದು ಮಾದರಿಯನ್ನು ಸ್ಥಾಪಿಸಿದರು, ಅದರ ಪ್ರಕಾರ ಸುರುಳಿಯಲ್ಲಿನ ಇಂಡಕ್ಷನ್ ಪ್ರವಾಹದ ದಿಕ್ಕನ್ನು ಮತ್ತು ಇಂಡಕ್ಷನ್ ಇಎಮ್ಎಫ್ ಅನ್ನು ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ. ಕಾಂತೀಯ ಹರಿವು ಬದಲಾದಾಗ ಸುರುಳಿಯಲ್ಲಿನ ಇಂಡಕ್ಷನ್ ಇಎಮ್ಎಫ್ ಸುರುಳಿಯಲ್ಲಿ ದಿಕ್ಕಿನ ಪ್ರವಾಹವನ್ನು ರೂಪಿಸುತ್ತದೆ ಎಂದು ಕಾನೂನು ಹೇಳುತ್ತದೆ, ಇದರಲ್ಲಿ ಸುರುಳಿಯ ನಿರ್ದಿಷ್ಟ ಕಾಂತೀಯ ಹರಿವು ಬಾಹ್ಯ ಕಾಂತೀಯ ಹರಿವಿನ ಬದಲಾವಣೆಗಳನ್ನು ತಪ್ಪಿಸಲು ಸಾಧ್ಯವಾಗಿಸುತ್ತದೆ.
ಲೆನ್ಜ್ ನಿಯಮವು ವಾಹಕಗಳಲ್ಲಿ ವಿದ್ಯುತ್ ಪ್ರವಾಹದ ಪ್ರಚೋದನೆಯ ಎಲ್ಲಾ ಸಂದರ್ಭಗಳಿಗೆ ಅನ್ವಯಿಸುತ್ತದೆ, ಅವುಗಳ ಸಂರಚನೆ ಮತ್ತು ಬಾಹ್ಯ ಕಾಂತೀಯ ಕ್ಷೇತ್ರವನ್ನು ಬದಲಾಯಿಸುವ ವಿಧಾನವನ್ನು ಲೆಕ್ಕಿಸದೆ.
ಕಾಂತಕ್ಷೇತ್ರದಲ್ಲಿ ತಂತಿಯ ಚಲನೆ
ಬಲದ ಕ್ಷೇತ್ರ ರೇಖೆಗಳಿಂದ ದಾಟಿದ ವಾಹಕದ ಉದ್ದವನ್ನು ಅವಲಂಬಿಸಿ ಪ್ರೇರಿತ EMF ನ ಮೌಲ್ಯವನ್ನು ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ. ಹೆಚ್ಚಿನ ಸಂಖ್ಯೆಯ ಕ್ಷೇತ್ರ ರೇಖೆಗಳೊಂದಿಗೆ, ಪ್ರೇರಿತ ಇಎಮ್ಎಫ್ ಮೌಲ್ಯವು ಹೆಚ್ಚಾಗುತ್ತದೆ. ಕಾಂತೀಯ ಕ್ಷೇತ್ರ ಮತ್ತು ಇಂಡಕ್ಷನ್ ಹೆಚ್ಚಳದೊಂದಿಗೆ, ವಾಹಕದಲ್ಲಿ ಇಎಮ್ಎಫ್ನ ಹೆಚ್ಚಿನ ಮೌಲ್ಯವು ಸಂಭವಿಸುತ್ತದೆ. ಹೀಗಾಗಿ, ಆಯಸ್ಕಾಂತೀಯ ಕ್ಷೇತ್ರದಲ್ಲಿ ಚಲಿಸುವ ಕಂಡಕ್ಟರ್ನಲ್ಲಿ ಇಂಡಕ್ಷನ್ನ ಇಎಮ್ಎಫ್ನ ಮೌಲ್ಯವು ನೇರವಾಗಿ ಕಾಂತಕ್ಷೇತ್ರದ ಇಂಡಕ್ಷನ್, ವಾಹಕದ ಉದ್ದ ಮತ್ತು ಅದರ ಚಲನೆಯ ವೇಗವನ್ನು ಅವಲಂಬಿಸಿರುತ್ತದೆ.
ಈ ಅವಲಂಬನೆಯು E = Blv ಸೂತ್ರದಲ್ಲಿ ಪ್ರತಿಫಲಿಸುತ್ತದೆ, ಅಲ್ಲಿ E ಇಂಡಕ್ಷನ್ emf ಆಗಿದೆ; ಬಿ ಕಾಂತೀಯ ಇಂಡಕ್ಷನ್ ಮೌಲ್ಯವಾಗಿದೆ; ನಾನು ಕಂಡಕ್ಟರ್ನ ಉದ್ದ; v ಅದರ ಚಲನೆಯ ವೇಗ.
ಆಯಸ್ಕಾಂತೀಯ ಕ್ಷೇತ್ರದಲ್ಲಿ ಚಲಿಸುವ ಕಂಡಕ್ಟರ್ನಲ್ಲಿ, ಇಂಡಕ್ಷನ್ ಇಎಮ್ಎಫ್ ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ರೇಖೆಗಳನ್ನು ದಾಟಿದಾಗ ಮಾತ್ರ ಕಾಣಿಸಿಕೊಳ್ಳುತ್ತದೆ ಎಂಬುದನ್ನು ಗಮನಿಸಿ. ಕಂಡಕ್ಟರ್ ಬಲದ ರೇಖೆಗಳ ಉದ್ದಕ್ಕೂ ಚಲಿಸಿದರೆ, ನಂತರ ಯಾವುದೇ EMF ಅನ್ನು ಪ್ರಚೋದಿಸಲಾಗುವುದಿಲ್ಲ. ಈ ಕಾರಣಕ್ಕಾಗಿ, ವಾಹಕದ ಚಲನೆಯನ್ನು ಬಲದ ರೇಖೆಗಳಿಗೆ ಲಂಬವಾಗಿ ನಿರ್ದೇಶಿಸಿದ ಸಂದರ್ಭಗಳಲ್ಲಿ ಮಾತ್ರ ಸೂತ್ರವು ಅನ್ವಯಿಸುತ್ತದೆ.
ವಾಹಕದಲ್ಲಿ ಪ್ರೇರಿತ ಇಎಮ್ಎಫ್ ಮತ್ತು ವಿದ್ಯುತ್ ಪ್ರವಾಹದ ದಿಕ್ಕನ್ನು ಕಂಡಕ್ಟರ್ನ ಚಲನೆಯ ದಿಕ್ಕಿನಿಂದ ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ. ದಿಕ್ಕನ್ನು ಗುರುತಿಸಲು, ಬಲಗೈ ನಿಯಮವನ್ನು ಅಭಿವೃದ್ಧಿಪಡಿಸಲಾಗಿದೆ. ನಿಮ್ಮ ಬಲಗೈಯ ಅಂಗೈಯನ್ನು ನೀವು ಹಿಡಿದಿದ್ದರೆ, ಕ್ಷೇತ್ರ ರೇಖೆಗಳು ಅದರ ದಿಕ್ಕಿನಲ್ಲಿ ಪ್ರವೇಶಿಸುತ್ತವೆ ಮತ್ತು ಹೆಬ್ಬೆರಳು ವಾಹಕದ ಚಲನೆಯ ದಿಕ್ಕನ್ನು ಸೂಚಿಸುತ್ತದೆ, ನಂತರ ಉಳಿದ ನಾಲ್ಕು ಬೆರಳುಗಳು ಪ್ರೇರಿತ ಇಎಮ್ಎಫ್ನ ದಿಕ್ಕನ್ನು ಮತ್ತು ವಿದ್ಯುತ್ ಪ್ರವಾಹದ ದಿಕ್ಕನ್ನು ಸೂಚಿಸುತ್ತವೆ. ಕಂಡಕ್ಟರ್ನಲ್ಲಿ.
ತಿರುಗುವ ಸುರುಳಿ
ವಿದ್ಯುತ್ ಪ್ರವಾಹ ಜನರೇಟರ್ನ ಕಾರ್ಯವು ಕಾಂತೀಯ ಹರಿವಿನಲ್ಲಿ ಸುರುಳಿಯ ತಿರುಗುವಿಕೆಯನ್ನು ಆಧರಿಸಿದೆ, ಅಲ್ಲಿ ನಿರ್ದಿಷ್ಟ ಸಂಖ್ಯೆಯ ತಿರುವುಗಳಿವೆ. ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಫಾರ್ಮುಲಾ Ф \u003d B x S x cos α (ಕಾಂತೀಯ ಹರಿವು ಹಾದುಹೋಗುವ ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣದಿಂದ ಗುಣಿಸಿದಾಗ ಕಾಂತೀಯ ಪ್ರಚೋದನೆ ಮತ್ತು ಕೊಸೈನ್) ಆಧಾರದ ಮೇಲೆ ಕಾಂತೀಯ ಹರಿವಿನಿಂದ ದಾಟಿದಾಗ EMF ಅನ್ನು ಯಾವಾಗಲೂ ವಿದ್ಯುತ್ ಸರ್ಕ್ಯೂಟ್ನಲ್ಲಿ ಪ್ರಚೋದಿಸಲಾಗುತ್ತದೆ. ದಿಕ್ಕಿನ ವೆಕ್ಟರ್ ಮತ್ತು ಲಂಬವಾದ ಸಮತಲ ರೇಖೆಗಳಿಂದ ರೂಪುಗೊಂಡ ಕೋನದ).
ಸೂತ್ರದ ಪ್ರಕಾರ, ಸಂದರ್ಭಗಳಲ್ಲಿ ಬದಲಾವಣೆಗಳಿಂದ ಎಫ್ ಪ್ರಭಾವಿತವಾಗಿರುತ್ತದೆ:
- ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಬದಲಾದಾಗ, ದಿಕ್ಕು ವೆಕ್ಟರ್ ಬದಲಾಗುತ್ತದೆ;
- ಬಾಹ್ಯರೇಖೆಯ ಬದಲಾವಣೆಗಳಲ್ಲಿ ಸುತ್ತುವರಿದ ಪ್ರದೇಶ;
- ಕೋನ ಬದಲಾವಣೆಗಳು.
ಸ್ಥಾಯಿ ಮ್ಯಾಗ್ನೆಟ್ ಅಥವಾ ಸ್ಥಿರವಾದ ಪ್ರವಾಹದೊಂದಿಗೆ EMF ಅನ್ನು ಪ್ರೇರೇಪಿಸಲು ಇದನ್ನು ಅನುಮತಿಸಲಾಗಿದೆ, ಆದರೆ ಕಾಂತೀಯ ಕ್ಷೇತ್ರದೊಳಗೆ ಸುರುಳಿಯು ಅದರ ಅಕ್ಷದ ಸುತ್ತ ತಿರುಗಿದಾಗ. ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಕೋನ ಬದಲಾದಂತೆ ಕಾಂತೀಯ ಹರಿವು ಬದಲಾಗುತ್ತದೆ. ತಿರುಗುವಿಕೆಯ ಪ್ರಕ್ರಿಯೆಯಲ್ಲಿ ಸುರುಳಿಯು ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ನ ಬಲದ ರೇಖೆಗಳನ್ನು ದಾಟುತ್ತದೆ, ಇದರ ಪರಿಣಾಮವಾಗಿ, ಇಎಮ್ಎಫ್ ಕಾಣಿಸಿಕೊಳ್ಳುತ್ತದೆ. ಏಕರೂಪದ ತಿರುಗುವಿಕೆಯೊಂದಿಗೆ, ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ನಲ್ಲಿ ಆವರ್ತಕ ಬದಲಾವಣೆಯು ಸಂಭವಿಸುತ್ತದೆ. ಅಲ್ಲದೆ, ಪ್ರತಿ ಸೆಕೆಂಡಿಗೆ ದಾಟುವ ಕ್ಷೇತ್ರ ರೇಖೆಗಳ ಸಂಖ್ಯೆಯು ನಿಯಮಿತ ಮಧ್ಯಂತರದಲ್ಲಿ ಮೌಲ್ಯಗಳಿಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ.
ಪ್ರಾಯೋಗಿಕವಾಗಿ, ಪರ್ಯಾಯ ವಿದ್ಯುತ್ ಜನರೇಟರ್ಗಳಲ್ಲಿ, ಸುರುಳಿ ಸ್ಥಿರವಾಗಿರುತ್ತದೆ, ಮತ್ತು ವಿದ್ಯುತ್ಕಾಂತವು ಅದರ ಸುತ್ತಲೂ ತಿರುಗುತ್ತದೆ.
ಇಎಮ್ಎಫ್ ಸ್ವಯಂ ಪ್ರೇರಣೆ
ಪರ್ಯಾಯ ವಿದ್ಯುತ್ ಪ್ರವಾಹವು ಸುರುಳಿಯ ಮೂಲಕ ಹಾದುಹೋದಾಗ, ಪರ್ಯಾಯ ಕಾಂತೀಯ ಕ್ಷೇತ್ರವು ಉತ್ಪತ್ತಿಯಾಗುತ್ತದೆ, ಇದು EMF ಅನ್ನು ಪ್ರೇರೇಪಿಸುವ ಬದಲಾಗುತ್ತಿರುವ ಕಾಂತೀಯ ಹರಿವಿನಿಂದ ನಿರೂಪಿಸಲ್ಪಟ್ಟಿದೆ. ಈ ವಿದ್ಯಮಾನವನ್ನು ಸ್ವಯಂ ಪ್ರೇರಣೆ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.
ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ವಿದ್ಯುತ್ ಪ್ರವಾಹದ ತೀವ್ರತೆಗೆ ಅನುಗುಣವಾಗಿರುವುದರಿಂದ, ಸ್ವಯಂ-ಇಂಡಕ್ಷನ್ ಇಎಮ್ಎಫ್ ಸೂತ್ರವು ಈ ರೀತಿ ಕಾಣುತ್ತದೆ:
Ф = L x I, ಇಲ್ಲಿ L ಎಂಬುದು ಇಂಡಕ್ಟನ್ಸ್ ಆಗಿದೆ, ಇದನ್ನು H ನಲ್ಲಿ ಅಳೆಯಲಾಗುತ್ತದೆ.ಇದರ ಮೌಲ್ಯವನ್ನು ಪ್ರತಿ ಯುನಿಟ್ ಉದ್ದದ ತಿರುವುಗಳ ಸಂಖ್ಯೆ ಮತ್ತು ಅವುಗಳ ಅಡ್ಡ ವಿಭಾಗದ ಮೌಲ್ಯದಿಂದ ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ.
ಪರಸ್ಪರ ಇಂಡಕ್ಷನ್
ಎರಡು ಸುರುಳಿಗಳು ಪಕ್ಕದಲ್ಲಿ ನೆಲೆಗೊಂಡಾಗ, ಅವರು ಪರಸ್ಪರ ಇಂಡಕ್ಷನ್ನ EMF ಅನ್ನು ವೀಕ್ಷಿಸುತ್ತಾರೆ, ಇದು ಎರಡು ಸರ್ಕ್ಯೂಟ್ಗಳ ಸಂರಚನೆ ಮತ್ತು ಅವುಗಳ ಪರಸ್ಪರ ದೃಷ್ಟಿಕೋನದಿಂದ ನಿರ್ಧರಿಸಲ್ಪಡುತ್ತದೆ. ಸರ್ಕ್ಯೂಟ್ಗಳ ಹೆಚ್ಚುತ್ತಿರುವ ಬೇರ್ಪಡಿಕೆಯೊಂದಿಗೆ, ಪರಸ್ಪರ ಇಂಡಕ್ಟನ್ಸ್ನ ಮೌಲ್ಯವು ಕಡಿಮೆಯಾಗುತ್ತದೆ, ಏಕೆಂದರೆ ಎರಡು ಸುರುಳಿಗಳಿಗೆ ಒಟ್ಟು ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ನಲ್ಲಿ ಇಳಿಕೆ ಕಂಡುಬರುತ್ತದೆ.
ಪರಸ್ಪರ ಪ್ರಚೋದನೆಯ ಹೊರಹೊಮ್ಮುವಿಕೆಯ ಪ್ರಕ್ರಿಯೆಯನ್ನು ನಾವು ವಿವರವಾಗಿ ಪರಿಗಣಿಸೋಣ. ಎರಡು ಸುರುಳಿಗಳಿವೆ, ಪ್ರಸ್ತುತ I1 ಒಂದು ತಂತಿಯ ಮೂಲಕ N1 ತಿರುವುಗಳೊಂದಿಗೆ ಹರಿಯುತ್ತದೆ, ಇದು ಕಾಂತೀಯ ಹರಿವನ್ನು ಸೃಷ್ಟಿಸುತ್ತದೆ ಮತ್ತು N2 ಸಂಖ್ಯೆಯ ತಿರುವುಗಳೊಂದಿಗೆ ಎರಡನೇ ಸುರುಳಿಯ ಮೂಲಕ ಹೋಗುತ್ತದೆ.
ಮೊದಲನೆಯದಕ್ಕೆ ಸಂಬಂಧಿಸಿದಂತೆ ಎರಡನೇ ಸುರುಳಿಯ ಪರಸ್ಪರ ಇಂಡಕ್ಟನ್ಸ್ ಮೌಲ್ಯ:
M21 = (N2 x F21)/I1.
ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಮೌಲ್ಯ:
F21 = (M21/N2) x I1.
ಪ್ರೇರಿತ ಇಎಮ್ಎಫ್ ಅನ್ನು ಸೂತ್ರದಿಂದ ಲೆಕ್ಕಹಾಕಲಾಗುತ್ತದೆ:
E2 = - N2 x dФ21/dt = - M21x dI1/dt.
ಮೊದಲ ಸುರುಳಿಯಲ್ಲಿ, ಪ್ರೇರಿತ ಇಎಮ್ಎಫ್ ಮೌಲ್ಯ:
E1 = - M12 x dI2/dt.
ಸುರುಳಿಗಳಲ್ಲಿ ಒಂದರಲ್ಲಿ ಪರಸ್ಪರ ಪ್ರಚೋದನೆಯಿಂದ ಪ್ರಚೋದಿಸಲ್ಪಟ್ಟ ಎಲೆಕ್ಟ್ರೋಮೋಟಿವ್ ಬಲವು ಯಾವುದೇ ಸಂದರ್ಭದಲ್ಲಿ ಇತರ ಸುರುಳಿಯಲ್ಲಿನ ವಿದ್ಯುತ್ ಪ್ರವಾಹದಲ್ಲಿನ ಬದಲಾವಣೆಗೆ ನೇರವಾಗಿ ಅನುಪಾತದಲ್ಲಿರುತ್ತದೆ ಎಂಬುದನ್ನು ಗಮನಿಸುವುದು ಮುಖ್ಯವಾಗಿದೆ.
ನಂತರ ಪರಸ್ಪರ ಇಂಡಕ್ಟನ್ಸ್ ಅನ್ನು ಸಮಾನವಾಗಿ ಪರಿಗಣಿಸಲಾಗುತ್ತದೆ:
M12 = M21 = M.
ಪರಿಣಾಮವಾಗಿ, E1 = - M x dI2/dt ಮತ್ತು E2 = M x dI1/dt. M = K √ (L1 x L2), ಇಲ್ಲಿ K ಎಂಬುದು ಎರಡು ಇಂಡಕ್ಟನ್ಸ್ ಮೌಲ್ಯಗಳ ನಡುವಿನ ಸಂಯೋಜಕ ಗುಣಾಂಕವಾಗಿದೆ.
ಟ್ರಾನ್ಸ್ಫಾರ್ಮರ್ಗಳಲ್ಲಿ ಮ್ಯೂಚುಯಲ್ ಇಂಡಕ್ಟನ್ಸ್ ಅನ್ನು ವ್ಯಾಪಕವಾಗಿ ಬಳಸಲಾಗುತ್ತದೆ, ಇದು ಪರ್ಯಾಯ ವಿದ್ಯುತ್ ಪ್ರವಾಹದ ಮೌಲ್ಯವನ್ನು ಬದಲಾಯಿಸಲು ಸಾಧ್ಯವಾಗಿಸುತ್ತದೆ. ಸಾಧನವು ಒಂದು ಜೋಡಿ ಸುರುಳಿಯಾಗಿದ್ದು ಅದು ಸಾಮಾನ್ಯ ಕೋರ್ನಲ್ಲಿ ಗಾಯಗೊಂಡಿದೆ. ಮೊದಲ ಕಾಯಿಲ್ನಲ್ಲಿನ ಪ್ರವಾಹವು ಮ್ಯಾಗ್ನೆಟಿಕ್ ಸರ್ಕ್ಯೂಟ್ನಲ್ಲಿ ಬದಲಾಗುತ್ತಿರುವ ಮ್ಯಾಗ್ನೆಟಿಕ್ ಫ್ಲಕ್ಸ್ ಮತ್ತು ಎರಡನೇ ಕಾಯಿಲ್ನಲ್ಲಿ ಪ್ರವಾಹವನ್ನು ರೂಪಿಸುತ್ತದೆ.ಎರಡನೆಯದಕ್ಕಿಂತ ಮೊದಲ ಸುರುಳಿಯಲ್ಲಿ ಕಡಿಮೆ ತಿರುವುಗಳೊಂದಿಗೆ, ವೋಲ್ಟೇಜ್ ಹೆಚ್ಚಾಗುತ್ತದೆ, ಮತ್ತು ಅದರ ಪ್ರಕಾರ, ಮೊದಲ ಅಂಕುಡೊಂಕಾದ ದೊಡ್ಡ ಸಂಖ್ಯೆಯ ತಿರುವುಗಳೊಂದಿಗೆ, ವೋಲ್ಟೇಜ್ ಕಡಿಮೆಯಾಗುತ್ತದೆ.
ವಿದ್ಯುತ್ ಶಕ್ತಿಯನ್ನು ಉತ್ಪಾದಿಸುವ ಮತ್ತು ಪರಿವರ್ತಿಸುವುದರ ಜೊತೆಗೆ, ಮ್ಯಾಗ್ನೆಟಿಕ್ ಇಂಡಕ್ಷನ್ನ ವಿದ್ಯಮಾನವನ್ನು ಇತರ ಸಾಧನಗಳಲ್ಲಿ ಬಳಸಲಾಗುತ್ತದೆ. ಉದಾಹರಣೆಗೆ, ಮ್ಯಾಗ್ನೆಟಿಕ್ ಲೆವಿಟೇಶನ್ ರೈಲುಗಳಲ್ಲಿ ಹಳಿಗಳಲ್ಲಿನ ಪ್ರವಾಹದೊಂದಿಗೆ ನೇರ ಸಂಪರ್ಕವಿಲ್ಲದೆ ಚಲಿಸುವ ರೈಲುಗಳು, ಆದರೆ ವಿದ್ಯುತ್ಕಾಂತೀಯ ವಿಕರ್ಷಣೆಯ ಕಾರಣದಿಂದ ಒಂದೆರಡು ಸೆಂಟಿಮೀಟರ್ಗಳಷ್ಟು ಹೆಚ್ಚು.
ಇದೇ ರೀತಿಯ ಲೇಖನಗಳು: